![jeanluc@[domainname],
where [domainname] is math point wisc point edu](Icons/jlt_email_wisc.gif){kind=icon}
| Lecture Room: | B102 VAN VLECK |
| Lecture Time: | TuTh 11:00–12:15 |
| Office: | 503 Van Vleck |
| Phone: | (608)263-4089 |
| Email: | |
| Office Hours: | 1:00–2:00 Tu, 2:00–3:00 Th, or by appointment. |
Here is the practice exam, Sam's solutions, and Yu's solutions.
Chapter, section, and page numbers refer to Thomas, 12th ed.
| lecture | date | sections | topic | homework |
| 1 | 09/02 | chapt. 1 | Functions | 1.1: 1–6, 7, 9, 10, 13, 15, 18, 21, 22, 24, 27, 30, 38, 39, 45, 49, 50, 54, 55, 58, 60, 63, 72 |
| 2 | 09/07 | 2.1–2.2 | Average value; limits | 2.1: 1, 3, 4, 6; 2.2: 1, 2, 3, 5, 7, 8, 11–22 |
| 3 | 09/09 | 2.2–2.3 | Limits (precise def'n) | 2.2: 23, 24, 26, 31, 32, 34, 37–40 (see example 9, p. 52), 43, 44, 48, 52, 55, 56, 63, 64 |
| 4 | 09/14 | 2.3–2.4 | Limits (precise def'n); One-sided limits | 2.3 2–5, 8, 9, 11, 16, 17, 18, 20, 21, 22, 23, 25, 31, 32, 35, 38, 42, 43 |
| 5 | 09/16 | 2.5 | Continuity | 2.4 1, 2, 4, 5, 8, 13, 14, 16, 18, 21–30; 2.5 1–10, 13–20, 26–30, 32–35, 39–44 |
| 6 | 09/21 | 2.6 | Limits and infinity | 2.6: 1, 2, 4–6, 10–12, 16–20, 26–32, 40–44, 50, 51, 55, 56, 65, 66, 82–84, 100–102 |
| 7 | 09/23 | 3.1–3.2 | Differentiation | 3.2: 3–6, 10–12, 14, 15, 18, 21, 22, 24, 27–30, 32, 36, 37, 38, 44–46 |
| 8 | 09/28 | 3.3 | Differentiation rules | 3.3: 1–7, 15, 16, 17, 19, 22, 23, 27, 31, 33–36, 41, 44. |
| 9 | 09/30 | 3.4–3.6 | Rate of change; Trig functions; Chain rule | 3.4: 2–5, 9, 12, 13, 23, 24, 25, 26; 3.5: 1–3, 7–10, 15, 16, 23, 26, 30, 31, 34, 37, 49, 50, 53, 57. |
| 10 | 10/05 | 3.7–3.8 | Implicit differentiation; Related rates | 3.6: 1–6, 15–18, 27–33, 47–51, 59, 62, 65, 68; 3.7: 1–9, 17, 22–25, 31–33, 41, 42. |
| 11 | 10/07 | — | Review and questions | |
| 12 | 10/12 | — | Midterm 1 | |
| 13 | 10/14 | 3.8–3.9 | Related rates; Linearization and differentials | 3.8: 1, 2, 11, 13, 14, 15, 18, 19, 29; 3.9: 1–3, 5, 6, 9–11, 14, 15, 17, 20, 25 |
| 14 | 10/19 | 4.1–4.2 | Extreme values; Mean value theorem | 4.1: 1–5, 8, 9, 11–14, 23, 25, 26, 28, 30, 31, 32, 35, 36, 38, 39, 41, 46, 47, 49, 52, 55, 60, 61, 65, 68; 4.2: 1, 4, 5, 7, 8, 11, 13. |
| 15 | 10/21 | 4.3–4.4 | First derivative test; Concavity | 4.3: 3–11, 15, 16, 28–31, 36, 37, 43, 44, 49, 51, 55, 60. |
| 16 | 10/26 | 4.4–4.5 | Applied optimization | 4.4: 1–6, 9, 12, 15, 23, 25, 29, 40, 47, 53, 75, 84, 87, 91. |
| 17 | 10/28 | 4.7 | Antiderivatives | 4.5: 1, 3, 8, 10, 14, 22, 27, 47 (d optional). 4.7: 1–5, 10–14, 21–26, 35–42, 49, 50, 57, 58, 62, 68, 69–72, 76–79, 81, 82, 95, 98. |
| 18 | 11/2 | 5.1–5.3 | Definite integrals | — |
| 19 | 11/4 | 5.3–5.4 | Area; Fundamental theorem | 5.3: 9, 10, 12, 14, 15, 20, 29, 31, 32, 36, 40, 43, 46, 47, 50, 51, 54, 56, 61, 72, 73, 75, 82. |
| 20 | 11/9 | 5.5–5.6 | Substitution | 5.4: 1–8, 21–28, 30, 31, 35, 36, 41, 42, 44, 47, 49; 5.5: 1–4, 10, 11, 14, 23–25, 37, 40, 42, 50, 51, 56. |
| 21 | 11/11 | 6.1 | Area between curves; Volumes | 5.6: 1–4, 9–12, 14, 15, 22, 19, 24, 25, 27, 33, 37, 41, 44, 47, 49, 52, 55, 61, 65, 69, 81; 6.1: 1, 2, 5, 7, 11, 14, 15, 17, 21, 25, 33, 34, 38, 43, 45, 51. |
| 22 | 11/16 | — | Review and questions | |
| 23 | 11/18 | — | Midterm 2 | |
| 24 | 11/23 | 6.2–6.3 | Volumes by shell method; Arc length | 6.2: 1, 4, 5, 9, 12, 14, 17, 21, 24, 28, 29, 34, 41. 6.3: 1, 2, 4, 6, 9, 19, 21. |
| 25 | 11/30 | 7.1 | Derivative of inverse functions | 7.1: 1–6, 8, 11, 12, 14, 18, 19, 22, 29, 31, 33, 35, 38, 42, 43. |
| 27 | 12/2 | 7.2 | Natural logarithms | 7.2: 1, 3, 5, 8–16, 29–34, 39–44, 55–60, 65–68. |
| 28 | 12/7 | 7.3–7.4 | Exponential functions | 7.3: 1, 3, 5, 11, 20, 23, 28, 29, 33, 35, 42, 43, 50, 51, 52, 55, 58, 63–69, 76, 83, 86, 91, 97, 101, 106, 108, 111, 114, 118. 7.4: 23, 25, 27, 30, 33. |
| 29 | 12/9 | 7.6 | Inverse trig functions | 7.6: 4, 5, 9, 12, 21, 26–30, 37–41, 43, 50, 53, 59, 65, 67, 73, 75, 79, 84. |
| 30 | 12/14 | — | Review and questions | |
| 31 | 12/16 | — | Mock final (optional) | From 11:00am to 1:00pm in usual classroom (bring paper to write on, since questions will be written on board) |
| Name | Office | Phone | |||
| Sam Eckels | 718 Van Vleck | 2-0079 | eckels | @ | math.wisc.edu |
| Ed Dewey | 420 Van Vleck | 2-3853 | dewey | @ | math.wisc.edu |
| Ting-ting Nan | 416 Van Vleck | 3-6258 | nan | @ | math.wisc.edu |
| Huanyu Wen | 620 Van Vleck | 2-3600 | wen | @ | math.wisc.edu |
| Yu Zeng | 620 Van Vleck | 2-3600 | zeng | @ | math.wisc.edu |
| Number | Time | Days | Room | TA |
| 340 | 7:45 | MW | B337 VAN VLECK | Ting-ting Nan |
| 342 | 8:50 | MW | B333 VAN VLECK | Huanyu Wen |
| 343 | 9:55 | MWF | 277 BASCOM | Sam Eckels |
| 344 | 9:55 | MW | B333 VAN VLECK | Ting-ting Nan |
| 346 | 11:00 | MW | B333 VAN VLECK | Ed Dewey |
| 348 | 12:05 | MW | B317 VAN VLECK | Ed Dewey |
| 349 | 13:20 | MW | B329 VAN VLECK | Yu Zeng |
| 350 | 11:00 | MW | B123 VAN VLECK | Huanyu Wen |
| 351 | 14:25 | MW | B203 VAN VLECK | Yu Zeng |
See the official list of topics from the textbook.
The textbook for the class is Thomas' Calculus, 12th edition (with 2nd-order differential equations; ISBN 9780321726414). Be careful about the version you buy: the university bookstore has the right one, but Amazon doesn't seem to carry this specific edition. We will cover chapters 1 to 7, inclusive.
If you want additional viewpoints, have a look at the excellent notes by Prof. J. W. Robbin and the equally-excellent notes by Prof. S. B. Angenent.
The official prerequisite is one of
You should be comfortable with basic algebra and trigonometry. If you want to do some revision beforehand, work through Chapter 1 of Thomas and of the lecture notes mentioned above.
If you want to check your basic algebra skills, you can take Prof. Robbin's pre-test, with answers.
Attend the Review Workshops (What are you expected to know in your math class?) if you are not sure you know enough precalculus.Each week I will assign homework from the textbooks and post it here (above). Each following Wednesday (starting Sept. 8), your TA will give a 20 min quiz during your discussion section, consisting of a few questions from or related to the previous few homeworks. This will make up part of your grade, as described below. The TA for your section might decide to collect some homework or have some additional methods of assessment, at their discretion.
Notes, textbooks, or calculators will not be allowed in the quizzes. At least one of your lowest quiz scores will be discarded, and there will be no make-up quizzes.
Even if it is not collected, you should do all of the homework if you want a chance to do well in the class.
There will be two midterm exams. Each of the two midterm exams is worth 20 percent, for a total of 40 percent of the final grade. The final exam will count for 40 percent. The remaining 20 percent is a Discussion Section grade allocated by your TA who will base it on homework, quizzes, participation, attendance, and effort. (The Discussion Section grade will be adjusted to account for variations among the TAs.)
| Midterm Exam I | 20% | (Tuesday October 12, 2010) | |
| Midterm Exam II | 20% | (Thursday November 18, 2010) | |
| Final Exam | 40% | (Wednesday December 22, 2010 at 7:45 A.M.) | |
| Discussion section grade | 20% |
Calculators, notes, and textbooks are not allowed in exams or quizzes. The intelligent use of calculators outside of exam rooms is however encouraged.
Read Christelle Vincent's math study guide.
There are many ways to get help with math. In addition, following these guidelines is a recipe for (but not a guarantee of) success:
| # of nonzero scores | 192 | (excluding WES) |
| mean score | 74 | |
| standard deviation | 16 | |
| median score | 77.5 |
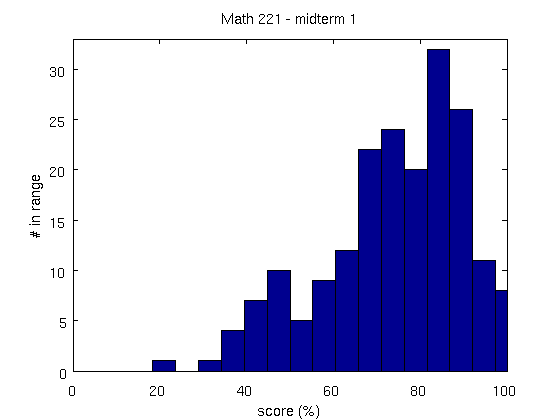
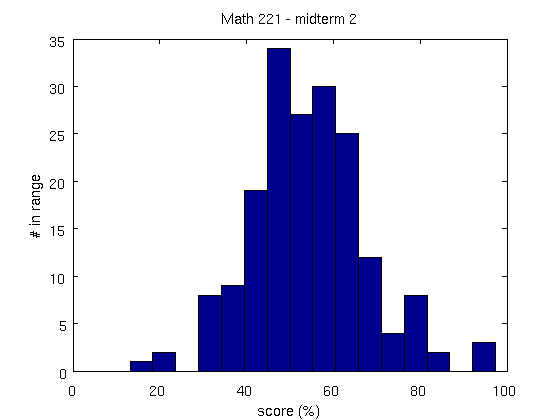
| # of nonzero scores | 184 | (excluding WES) |
| mean score | 54% | |
| standard deviation | 13 | |
| median score | 54 |
Letter grade ranges:
| grade | cut-off score (%) |
| A | ≥ 70 |
| AB | ≥ 64 |
| B | ≥ 56 |
| BC | ≥ 50 |
| C | ≥ 44 |
| D | ≥ 39 |
| F | < 39 |
Class grade average: 2.41 (roughly BC)
|
|
Last modified: 16:01 20 April 2021 |
Background: Coarsening of a binary fluid (Simulations by Lennon Ó Náraigh) |
Follow @jeanluc_t |
|