Math 234 — Homework Assignments

Week fourteen
Read: Ch7–§9, 10, 11
Do: Ch7–§12: problems 1, 2, 3, 4, and 5. For each line integral in Ch7–§12, problem 5,

• compute the integral in two ways, as stated in the problem;
• interpret the integral as a work integral $\int_{C} \mathbf{\vec F} \cdot \mathbf{\vec T}\; ds$ and find the force vectorfield $\mathbf{\vec F}$
• interpret the integral as a flux integral $\int_{C} \mathbf{\vec v} \cdot \mathbf{\vec N}\; ds$ and find the velocity vectorfield $\mathbf{\vec v}$

Week thirteen
Read: Ch7–§1, 2, 3, 5, 6, 7
Do:

• §4: problems 1, 2, 3, 4, 5
• §8: problems 1, 2, 3, 4

Week twelve
Read: Ch6–§4,5,6
Do:

• Ch.6, §3, page 122: Problems 9, 10.
• Ch.6, §7, page 134: Review problems 1, 2, 3, 4.
• Ch.6, §7, page 135: Problems 5, 6.
• Ch.6, §7, page 135: Problem 7. For problems 7c and 7d it is good to know Thales’ Theorem, the oldest math theorem according to some. Read the first paragraph and look at the first picture on the Wikipedia page about Thales’ theorem. What are the polar coordinates of the point B if we call A the origin? I.e. if the diameter AC is 1, and if the angle A is θ, then how much is the radius AB?

Week eleven
Read: Ch6–§1,2
Do: Ch.6, §3, page 122: Problems 1,2,3,4 (was done in lecture), 5acfh, 6ade, 7, 8a

Week nine
Read: Ch5–§12
Do: Ch.5, §10, page 102: Problems, 5cdh, 7bc.
Ch.5, §13, page 107: Problems 1, 2, 5a, 6a, 9, 10

Week eight:
Read Ch5–§7, Ch5–§9
Do: Ch.5, §8, page 96: Problem 1
Ch.5, §10, page 102: Problems 1, 2abcd, 4&8, 5abemnpq, 5f, 7a

Week seven: Ch.V, §3, page 89: Problems 1, 2, 3
§6, page 94: Problems 1abefm, 2, 5!

Week six: Ch.IV, §12, page 80: Problems 9abcd, 10
§15, page 85: Problems 1, 2, 4, 5, 6, 9, 12, 13, 15.

Week five: Ch.IV, §3, page 55/56: Problems 1abc, 2abcfgh, 3ab, 4a, 6.
§7, page 65: Problems 1, 2.
The following graphs were made with the Mac Grapher (download the grapher files to a mac to start up the grapher). For windows a free 3D graphing calculator is available at the Graphcalc website. Graphcalc runs on Windows XP, vista, and 7 (I don't know about windows 8 yet), and it lets you make pictures similar to these:

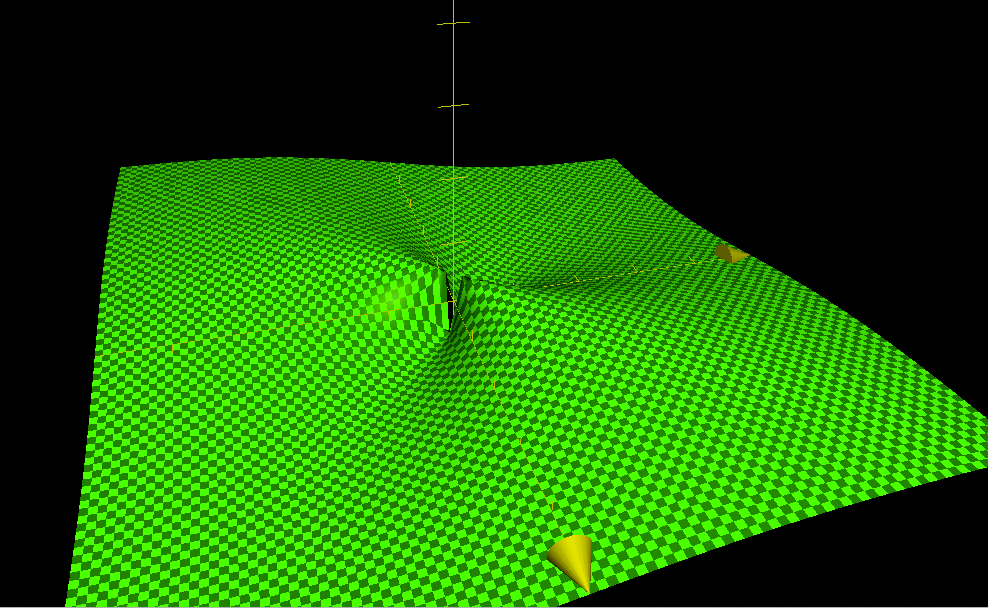
	Problem 1a. The question is if the limit of z=xy/(x2+y2) as (x,y)→(0,0) exists. The graph shows that you can get different limits, depending on the path you take. For example, if you set y=0 and let x→0, then f(x, 0) = 0, so the limit is zero. If you set y=x, then f(x, y) = f(x,x) = ½, and the limit is +½ (the top ridge in this graph). If on the other hand you set y=-x, then f(x,y) = f(x, -x) = -½, and the limit is -½ (the valley approaching the z-axis in the figure). Since the limit of the function depends on how we let (x,y) go to (0,0), we say that the function has no limit at the origin. The Mac Grapher file that makes this picture
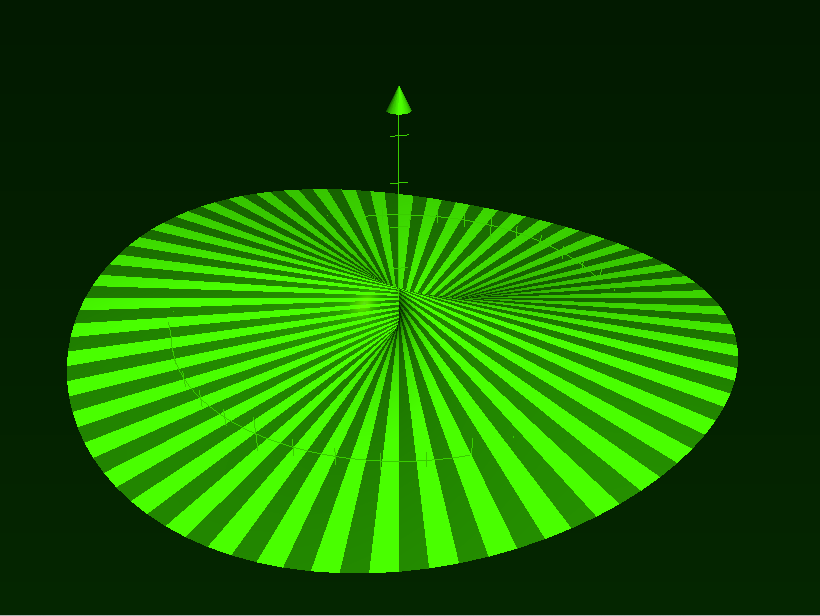
	Problem 1a (continued). One TA explained this graph by using polar coordinates. If you set x=r cosθ, y=r sinθ, then you get z=xy/(x2+y2)= sinθ cosθ = ½ sin 2θ For more details have a look at Chapter 3, §4.2. Mac Grapher file
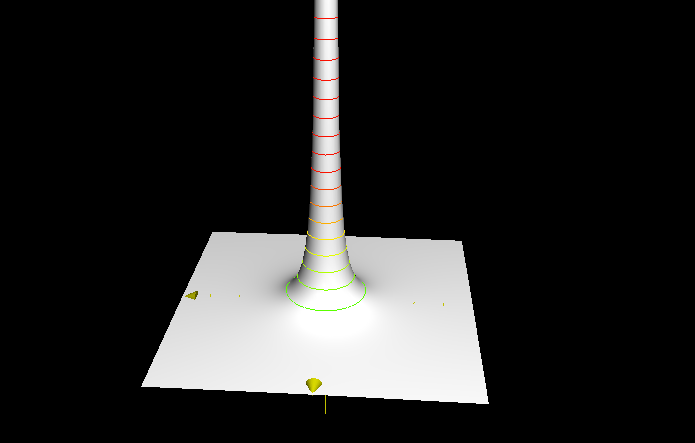
	Problem 1b. The function z=1/(x2+ y2) becomes infinite as x and y both go to zero, i.e. as (x,y)→(0,0). Mac Grapher file

Week four: Ch III, page 50/51: Problems 2, 3ab, 4, 5a–g, 7a–g, 11cd, 14abcfg.

Week three: Ch II, §17: Problems 3, 4, 5, and the problems on the second worksheet
Problem 3(a) as well as the construction of the cycloid will be done in lecture on Monday.
Quiz on these problems will be in discussion on Thursday Sept 19.

Week two: Ch I, §12: Problems 1, 2, 3, 4, 5, 6, 7, 8ab, 9a.
Quiz on these problems will be in discussion on Thursday Sept 12.

Week one: No homework, but we will be working from the first worksheet

Solutions to the first worksheet