Here is a STUDY GUIDE for the final exam.

Wednesday December 3: By examples I will show how to use the methods of "washers" and "shells" to compute volumes of solids of revolution. See §59 and 60 of the notes.

Problems for solution: 475—486 on page 120.

Monday December 1: I explained how you compute volumes by the method of slicing, and derived the first formula for the volume of a solid of revolution. All this is written up in the notes at §58 and §59.

Wednesday November 26: As an example I showed how to compute the volume of a cone.

Monday November 24: I computed a number of different integrals, showing how to use the method of substitution in various different ways. On Wednesday I will show how to differentiate a definite integral in which the upper and lower bounds depend on some variable. In particular, I'll explain the error function example in the notes (§55).

Friday November 21: We saw the difference between the definite and indefinite integrals, how to use the fundamental theorem to compute basic integrals, and we saw the method of substitution.

Wolfram's website will provide you an antiderivative whenever one can be found. You may have to work to transform the answer into your own answer. (Wolfram's site contains advertising and the presence of this link on this page is not intended as an endorsement of Mathematica®)

Problems: 330—460 (a huge list! Save a few for a rainy day.)

Answers and comments on the second midterm.

Here are the scores from the second midterm.

Your numeric score is what we record. At the end of the semester all your scores are added, after which we turn your total score into a letter grade. If the grade were only based on the midterm score the following conversion would be applied:

A 87-100; AB 82-86; B 73-81; BC 68-72; C 60-67; D 50-59; F <50

The exam will be from 7¹⁵pm—8⁴⁵pm in the following locations (look carefully):
Lecture 3 will have its exam at 125 Agriculture Hall, address 1450 Linden drive.
Lecture 4 (the 11am lecture) will have its exam at 2103 Chamberlin hall, address 1150 University Ave.

Friday Nov 14: I stated the definition of the integral of a function in terms of Riemann-sums. You can read this definition in the notes §50, page 99. Problems which you could look at for now are:

The integral as an area, and in terms of Riemann sums: 330, 331, 332, 364, 365.

Using the fundamental theorem to comppute integrals or areas: 333—363.

Wednesday Nov 12: We computed the area of the region caught between the graph of y = x² and the x axis, with 0<x<1. The reasoning used is the same that will allow us to prove the fundamental theorem of calculus on wednesday the 19th.

The midterm approaches! Here are a study guide and an old exam with solutions.

Monday Nov 10: We finished the chapter on exponential functions by looking at exponential growth. The main point was that any function X(t) whose relative growth rate X '(t)/X(t)=k is constant must be an exponential function of the form X(t) = X₀ e^kt.

Friday Nov 7: This lecture was about comparing functions at x=∞. Exponential functions grow faster than polynomial functions, and powers x^a grow faster than the logarithm ln x.

Wednesday Nov 5: Today's lecture was brought to you by the number e. You can find a picture and description of the Bell curve (graph of y = e ^{- x2}) on Wikipedia. The graph of this function is also the curve which is meant when people say they grade on a curve [wikipedia again].

On friday we look at limits involving e^x and we'll see how exponential growth always beats polynomial growth in the long run. To read ahead see §48, §49.

Monday Nov 3: I reviewed a^x and log_ax, and showed that the derivative of f(x) = 2^x is C2^x for some constant C = .693 147….

You, the student, should now know how to compute the derivative of f(x) = 4^x, f(x) = 8^x or f(x) = (½)^x.

In the notes I am now somewhere in the middle of §46. On wednesday I will explain §47 and §48.

Friday Oct 31: Optimization problems are the word problems that belong in the graphsketching chapter. To practice solving them try doing the problems 261—281 on page 85/86 of the notes.

On monday I will start with logarithms and exponential functions. Since these are covered in algebra, I will only briefly review logarithms, and spend much of the hour explaining how to differentiate f(x) = a^x.

Thursday Oct 30, 1:46pm: The answer sheet has again been updated. See also the errata page.

Wednesday October 29: I explained what the second derivative of a function tells you about its graph, and how you can tell if stationary point of a function is a local min or max. See §39. On friday I will discuss optimization problems, and , if time permits, go on to logarithms and exponential functions.

Monday October 27: In two examples I showed how to find local and global maxima/minima of a function. There was some confusion about what a global minimum is — read the beginning of §35 again to see the definition, and then think about the problem I did in class again (find the global maxima of f(x) = 3x-x³ with -2≤x≤2).

Problems to work on: 218—268. This is a long list of problems. Don't do all of them, but make sure you do a few of each type.

Friday October 24: I discussed when a function must have a global minimim or maximum. Read §35 and §36.

Wednesday October 22: Guest lecture by prof. Joel Robbin on the Mean Value Theorem.

Click here for an updated updated answer sheet (Thursday Oct 23, 10pm), and here for a list of typos in the notes which have been found.

Click here for an updated answer sheet.

Monday October 20: We started on chapter 5, and I explained the Intermediate Value Theorem. To prepare for next lecture read the section on increasing/decreasing functions, and the Mean Value Theorem.

At this point you should start looking at all remaining problems from chapter 4 (pages 65, 66).

October 13—17: I covered the method of implicit differentiation, and in particular found the derivatives of the Arc Sine and Arc Tangent. I also did two examples of so-called related rate problems.

Friday October 10: We did the derivatives of Sine, Cosine and Tangent, and we started on the chain rule. To read ahead look at § 28. (which I'll cover on monday.)

Suggested problems : Trig derivatives: 134—148 (page 55). Chain rule: 149—166 (page 61/62).

Here are the scores from the first midterm.

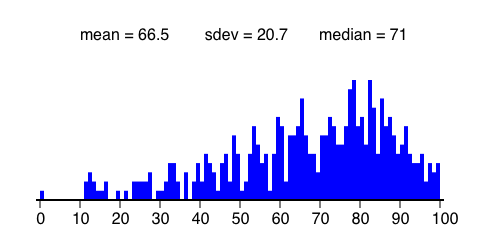
Your numeric score is what we record. At the end of the semester all your scores are added, after which we turn your total score into a letter grade. For some students we are required to report a temprorary 6-week (letter)grade. Your TA will assign this grade. If the grade were only based on the midterm score the following conversion would be applied:

A 87-100; AB 82-86; B 73-81; BC 68-72; C 60-67; D 50-59; F <50

Wednesday October 8: I gave a derivation of the quotient rule and of the derivative of x^p/q. These derivations illustrate the method of implicit derivation (see §29).

Monday October 6: I answered questions about the midterm exam. The exam will be from 7pm—8³⁰pm in the following locations (look carefully):
Lecture 3 will have its exam at 2103 Chamberlin hall, address 1150 University Ave.
Lecture 4 (the 11am lecture) will have its exam at 125 Agriculture Hall, address 1450 Linden drive.

For directions you can use Google maps or the UW's own campus map (type the buidling name in the box on the upper right of the UW campus map).

Last year's midterm (with answers) can be found right here.

To prepare for the FIRST MIDTERM you could look at this study guide.

Friday October 3: Explained the product rule (see figure 13, page 50 of the notes), the product rule for products of many functions, and the power rule. I stated the quotient rule and will give a proof next time.

On monday I will review material for the midterm (come with questions!). To read ahead for wednesday's lecture review the product and quotient rule material in §25.

Suggested problems: 108—122 (to practice computing derivatives), 123 (I will do one just like that in class), 124 (for fun…it's a way to make the product and quotient rules look more like each other, and nicer in general),125, 126.

Wednesday October 1: Did an example like problem 103 in the notes. Then started on the derivative rules.

Monday September 29: We saw a number of functions whose derivative doesn't exist a some or even at all points. Problems 101—107 are the last ones that are relevant to the first midterm.

Pictures of nowhere differentiable functions. These are function for which the derivative f'(x) does not exist, for any value of x. Here is one of Weierstrass' examples: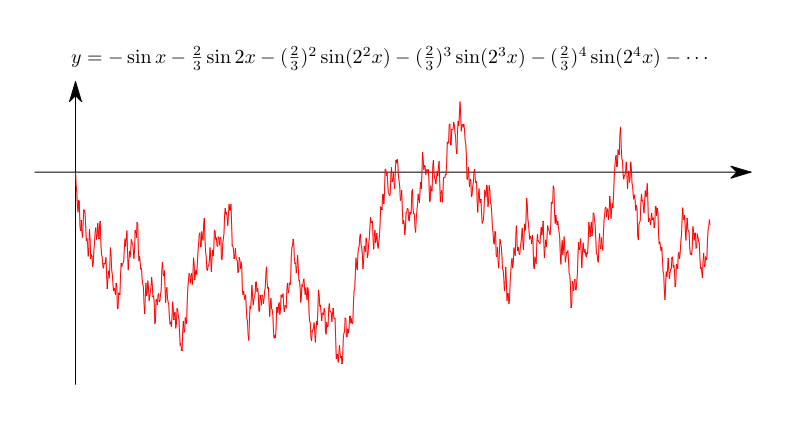

Another picture: The Dow-Jones index tends to produce figures that are very reminiscent of Weierstrass' function above.

Friday, sept 26. We computed the derivative of xⁿ, and reviewed the Geometric sum formula.

Suggested reading: §22, §23. (those are the last sections that will cover exam material.)

Suggested homework problems: 101—107.

Wednesday, sept 24. Now that we have learnt what the limit of sin(θ)/θ is, we are done with the chapter on Limits. On friday we start looking at derivatives again.

Suggested reading: §20, §21, §22. More importantly, do you remember the Geometric sum formula?

Monday, sept 22. I showed how to argue that a limit does not exist from the limit properties using “proof by contradiction.” For a few examples see §14.4, 14.5 and 14.6

Then we saw how the Sandwich theorem allows you to prove that some limits do exist (read §16). Today's last topic was Continuous Functions, see §17. (Draw the graph of the function in §17.5).

To read ahead look at §18 and 19.

Recommended homework problems (once you've digested §19): 77—99.

Friday, sept 19. We saw some examples of limit computations, in particular how to compute limits at ∞ of rational functions (§13.5, 13.6 in the notes), and then looked at a few different ways that a limit might fail to exist — see §14.1–3.

To read ahead, look at §14.4, 14.5 and 14.6. §15 makes the important distinction between free and dummy variables. Read this carefully, it will save you from a lot of confusion in the future.

Suggested problems : 52—66, 74, 75 (to practice the limit properties.)
67 (get familiar with the backward sine graph)
68,69,70,71,72 (logic! read the definitions and the limit properties)
76.

Thursday, sept 18. A few misprints in the answer sheet were reported (thanks to all who did so), and I have added a few more answers to the sheet. Here is the updated answer sheet.

Wednesday, sept 17. I covered variations on the limit theme (left and right hand limits, limit as x goes to infinity), and then introduced the basic limit properties. I have covered all examples in §13 through 13.4. To read ahead go through §13 and 14.

Monday, sept 15. I showed in two examples how you can use the ε–δ definition of limit to prove that lim x² = 4 as x approaches 2. This involved the “never choose δ > 1 trick” . Examples similar to the ones I did in class are in §10.2, and §10.3.

The previously posted answer sheet also contains solutions to some of the ε–δ problems in this section. Click here for an updated version (I removed a few misprints.)

Friday, sept 12. I stated the precise definition of the limit, and illustrated the meaning of epsilon and delta in terms of errors in reading a temperature in Celcius and converting it to Fahrenheit. On monday I will do several more abstract examples.

To read ahead for tomorrow's lecture , look at section 10.
Suggested problems: 38, 50 (again about measurement errors)
39—49.
51 (to think about)

Wednesday, sept 10. Described “rate of change,” and began discussing how one defines the limit of f(x) as x approaches a number a. On friday we will look at the precise definition of what a “limit” is. Be prepared, read §9 and carefully read § 10.1, 10.2, and have good look at the figure after §10.2.

Tuesday, sept 9. Here are answers to some of the problems in the notes. Since your TA will want to assign problems from the notes the list will not contain more than half the answers, and for most problems only short answers will be given rather than solutions. I will keep adding answers to this list and post them here during the semester.

Monday, September 8: I discussed what a tangent to a curve is, and showed how one computes the slope of a tangent. This material is in sections 4 and 5 of the notes. On wednesday I will go over sections 6 and 7.

Recommended problems:
27, 28, 30, 31 (to see if you understood §4 & §5).
29 (about round-off error; I will discuss this in lecture).
32, 33 (about units.)
34 ((b) is probably hard, see the answer).
35, 36, 37 (after you reduce these to algebra they shouldn't be harder than 30, 31).

Graphing Calculators. On exams you won't be using a graphing calculator, but for some homework assignments they can be handy. Even if you have a graphing calculator it is good to know that you can probably find a nicer calculator on your computer.

If you have a Mac (with OS X), then there is a very nice graphing calculator hidden in the utilities folder: just open Applications->Utilities and you'll find grapher.app.

If you have a windows computer then it doesn't come with a graphing calculator, but you can download one (for free) from the following link: GraphCalc

Friday, September 5. I discussed implicitely defined functions, inverse functions and in particular inverse trig functions (arcsin and arctan). I also pledged never to mention the dreaded secant function again.

A link to the math tutorial program which has LOTS of information on the kinds of outside help you can get for this class.

Some TAs are posting their own web pages with information relevant to their discussion sections:
Michael Woodbury | Seth Meyer | Esra Yeniaras

Wednesday, September 3. I covered section 2 and 3. On friday I intend to discuss implicitly defined functions, inverse functions, and briefly review the trig functions and their inverses. To read ahead look at §3 (pages 11—14.):
Recommended homework for this week:
4, 5, 6, 7 (what you should know about sets. page 8).
8—13, 18 (page 14, about implicitly defined functions)
14—17 (trig and inverse trig review)
19, 20, 21 (to see if you understand function notation)
22, 23, 24 (review of precalculus involving ax²+bx+c).