Research

My interests lie at the interface between fluid and solid structures in soft biological matter. The dynamics of bodies immersed in fluids at small scales is of great practical and biological interest, but fluid interactions on such scales are inherently nonlocal so their analysis and even computation can still be very challenging. I approach problems in biological propulsion, cell mechanics, and fluid-body interaction systems using a number of techniques, from the application of classical methods of applied mathematics to the development of novel numerical methods. Topics of recent interest include:

Microorganism / microscale locomotion

Swimming in complex fluids

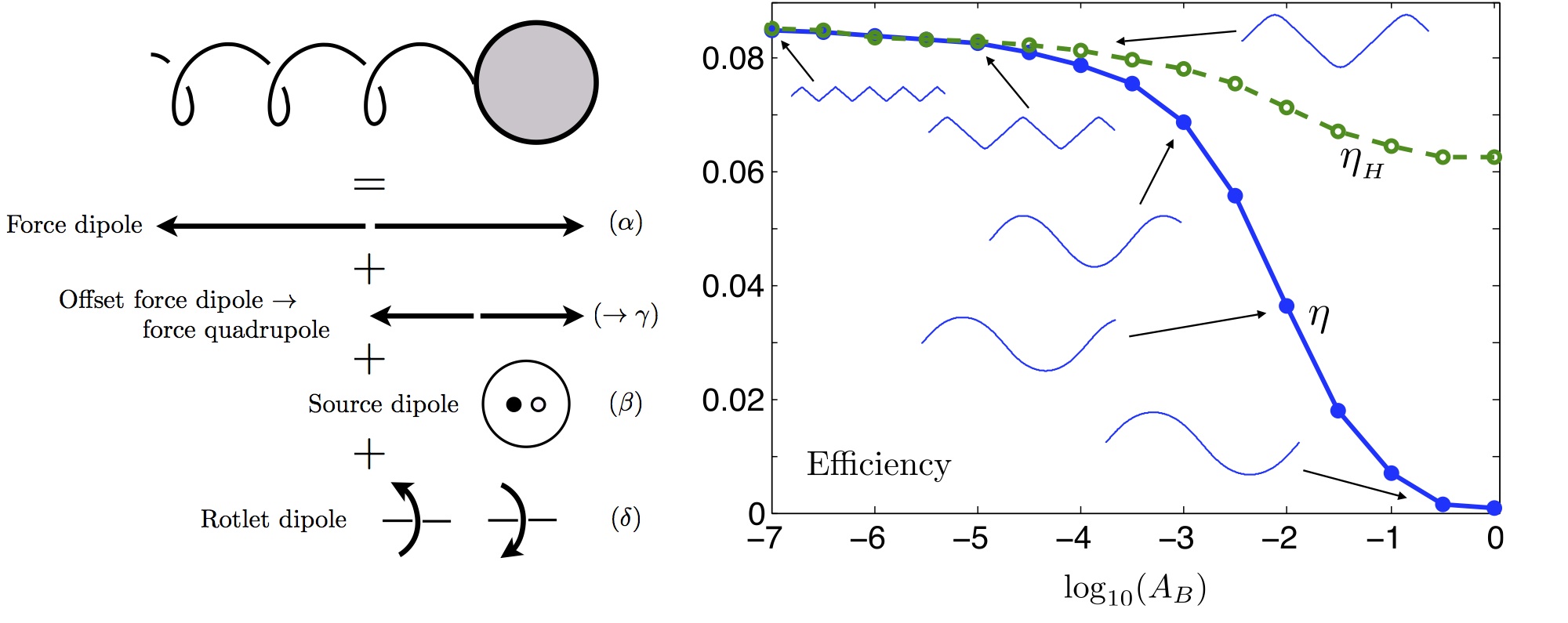
On scales relevant to most microorganisms, inertial effects are dominated by viscous dissipation; hence, the ejection of momentum into the fluid by the shedding of vortices, as observed in the locomotion of fish and birds, is not a viable means of propulsion for bacteria and spermatozoa. Understanding the nonlocal hydrodynamics of flagellar and ciliary locomotion in viscous fluids remains a topic of very active research - many important questions on the topics of optimization, surface effects, the collective dynamics of active suspensions, and the consequences of other physical effects including body flexibility, Brownian fluctuations, and internal molecular motor dynamics on locomotion remain unanswered.

Papers:

W. Lough, D.B. Weibel and S.E. Spagnolie, Self-buckling and self-writhing of semi-flexible swimmers, Soft Matter, 19, 7349-7357 (2023).

Z. Zou, W. Lough, and S.E. Spagnolie, Helical trajectories of swimming cells with a flexible flagellar hook, Phys. Rev. Fluids, 6, 103102 (2021).

C.J. Miles, A.A. Evans, M.J. Shelley, and S.E. Spagnolie, Active matter invasion of a viscous fluid: Unstable sheets and a no-flow theorem, Phys. Rev. Lett., 222, 098002 (2019).

S.E. Spagnolie, C. Wahl, J. Lukasik, and J.-L. Thiffeault, Microorganism Billiards, Physica D, 341, 33-44 (2017).

S.E. Spagnolie, G. Moreno-Flores, D. Bartolo, and E. Lauga, Geometric capture and escape of a microswimmer colliding with an obstacle, Soft Matter, 11, 3396 - 3411 (2015).

R. Chinomona, J. Lajeunesse, W.H. Mitchell, Y. Yao, and S.E. Spagnolie, Stability and dynamics of magnetocapillary interactions, Soft Matter, 11, 1828-1838 (2015).

L. Li and S.E. Spagnolie, Swimming and pumping by helical waves in viscous and viscoelastic fluids, Phys. Fluids, 27, 021902 (2015).

L. Li and S.E. Spagnolie, Swimming and pumping of rigid helical bodies in viscous fluids, Phys. Fluids, 26, 041901 (2014).

S.E. Spagnolie and E. Lauga, Hydrodynamics of self-propulsion near boundaries: predictions and accuracy of far-field approximations, J. Fluid Mech., 700, 105-147 (2012).

O.S. Pak, S.E. Spagnolie, and E. Lauga, The hydrodynamics of the double-wave structure of insect spermatozoa, J. R. Soc. Interface, 9, 1908-1924 (2012).

S.E. Spagnolie and E. Lauga, Comparative hydrodynamics of bacterial polymorphism, Phys. Rev. Lett., 106, 058103 (2011).

A. Evans, S.E. Spagnolie, and E. Lauga, Stokesian jellyfish: Locomotion of a bilayer vesicle, Soft Matter, 6, 1737-1747, (2010).

S.E. Spagnolie and E. Lauga, The optimal elastic flagellum, Phys. Fluids, 22, 031901, (2010).

S.E. Spagnolie and E. Lauga, Jet propulsion without inertia, Phys. Fluids, 22, 081902 (2010).

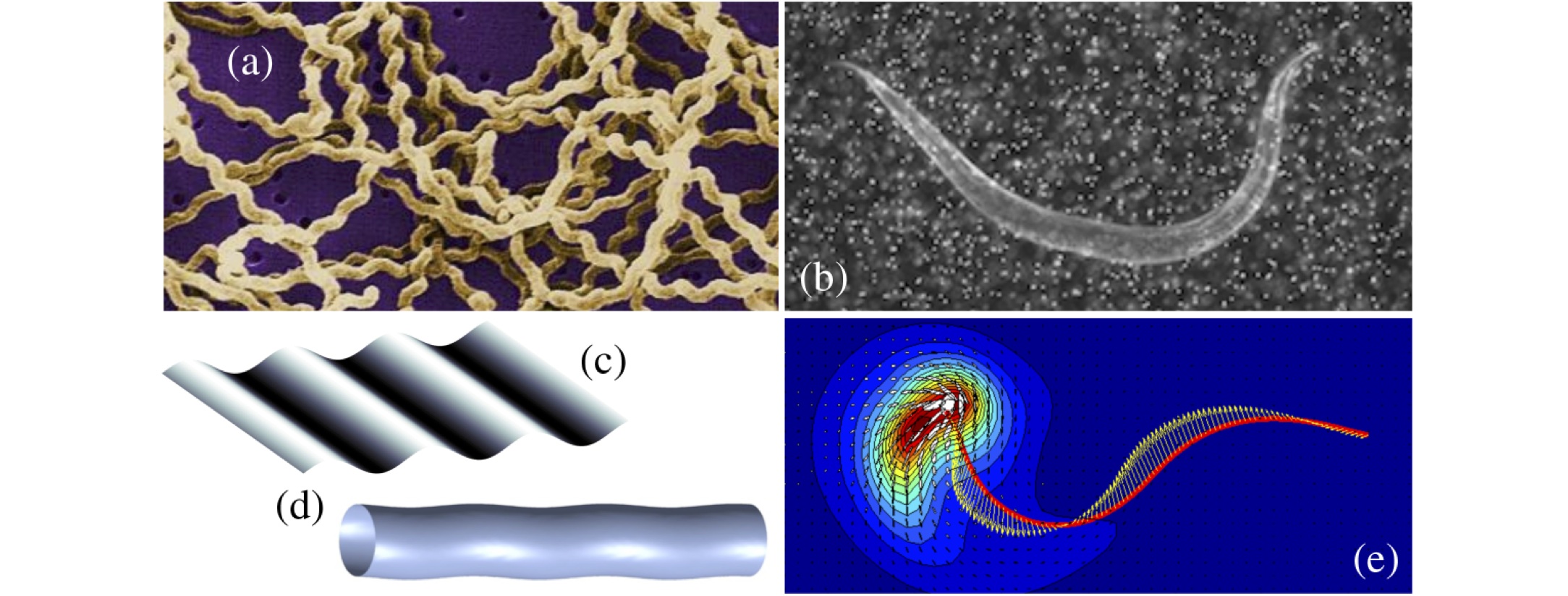
S.E. Spagnolie, Rehinging bi-flagellar locomotion in a viscous fluid Phys. Rev. E, 80, 046323 (2009).

Many organisms commonly swim in shear-thinning or viscoelastic biofluids, including mammalian spermatozoa in cervical fluid, and the Lyme disease spirochete B. burgdorferi in the extracellular matrix of our skin. Understanding the intricate interactions between complex fluid flows and flexible biological structures is a highly challenging and exciting current aim in mathematical biophysics. Images: (a) Leptospira (J. H. Carr, CDC, 2013); (b) C. elegans (courtesy of X. N. Shen and P. E. Arratia); (c,d) Taylor's swimming sheet and cylindrical analogue; (e) finite amplitude undulation (courtesy of J. Teran, L. Fauci, and M. Shelley).

Papers:

S.E. Spagnolie and P.T. Underhill, Swimming in Complex Fluids, Annu. Rev. Condens. Matter Phys., 14, 381-415 (2023).

M.S. Krieger, S.E. Spagnolie and T.R. Powers, Swimming with small and large amplitude waves in a confined liquid crystal, J. Non-Newtonian Fluid Mech., 273, 104185 (2019).

R.R. Trivedi, R. Maeda, N.L. Abbott, S.E. Spagnolie, and D.B. Weibel, Bacterial transport of colloids in liquid crystalline environments, Soft Matter, 11, 8404 - 8408 (2015).

M.S. Krieger, S.E. Spagnolie and T.R. Powers, Microscale locomotion in a nematic liquid crystal, Soft Matter, 11, 9115 - 9125 (2015).

L. Li and S.E. Spagnolie, Swimming and pumping by helical waves in viscous and viscoelastic fluids, Phys. Fluids, 27, 021902 (2015).

M.S. Krieger, S.E. Spagnolie and T.R. Powers, Locomotion and transport in a hexatic liquid crystal, Phys. Rev. E, 90, 052503 (2014).

S.E. Spagnolie, B. Liu and T.R. Powers, Locomotion of helical bodies in viscoelastic fluids: enhanced swimming at large helical amplitudes, Phys. Rev. Lett., 111, 068101 (2013).

Complex fluids in biological systems

Sedimentation in viscous fluids

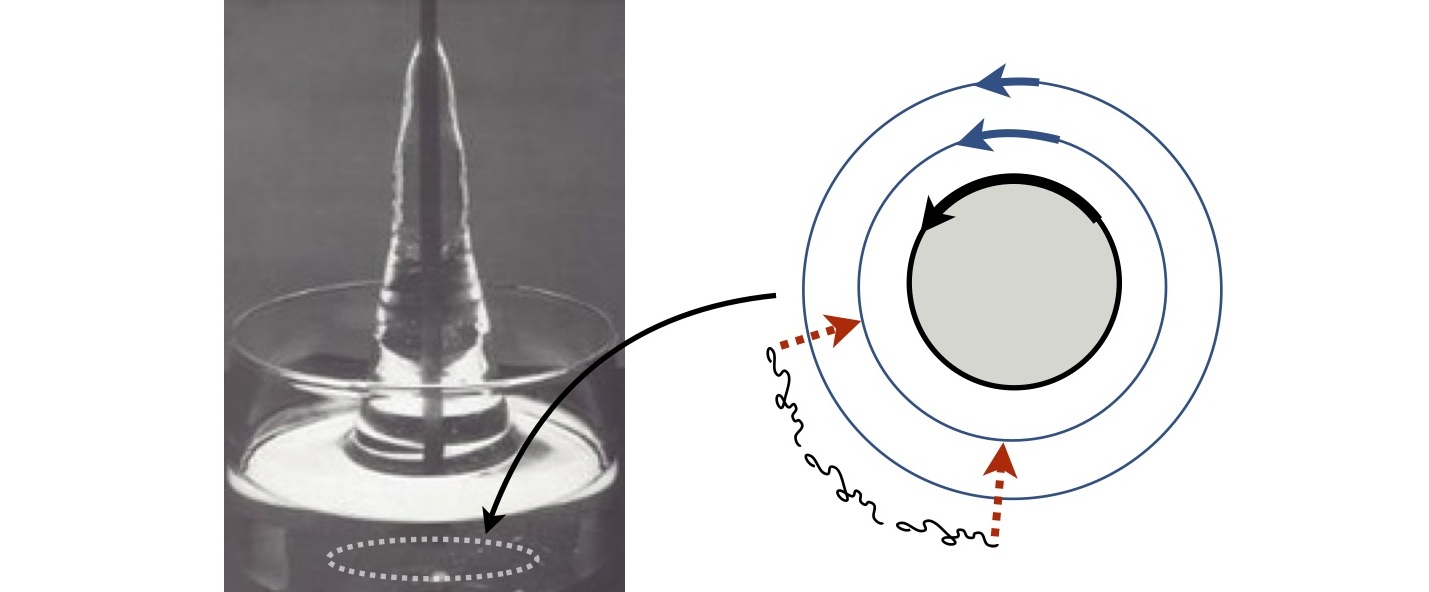
The complexity of biological systems is extraordinary, and so at the outset from a mathematical modeling point of view, daunting. Even the continuum approximations that give rise to the classical equations of fluid and solid mechanics do not survive the intricacy of biological matter, and the systems of equations describing the relevant flows, deformations, and stresses are coupled and nonlinear. Nevertheless, with the introduction of a more involved microstructure, such as the inclusion of long chain molecules (e.g. DNA, proteins, microtubules, etc.), continuum assumptions are commonly made to make mathematical modeling and analysis possible. The continuum approach has already become an invaluable approach to modeling and understanding real biological systems. Image: Viscoelastic rod-climbing (Boger and Walters, 1993), and illustration of "hoop stress."

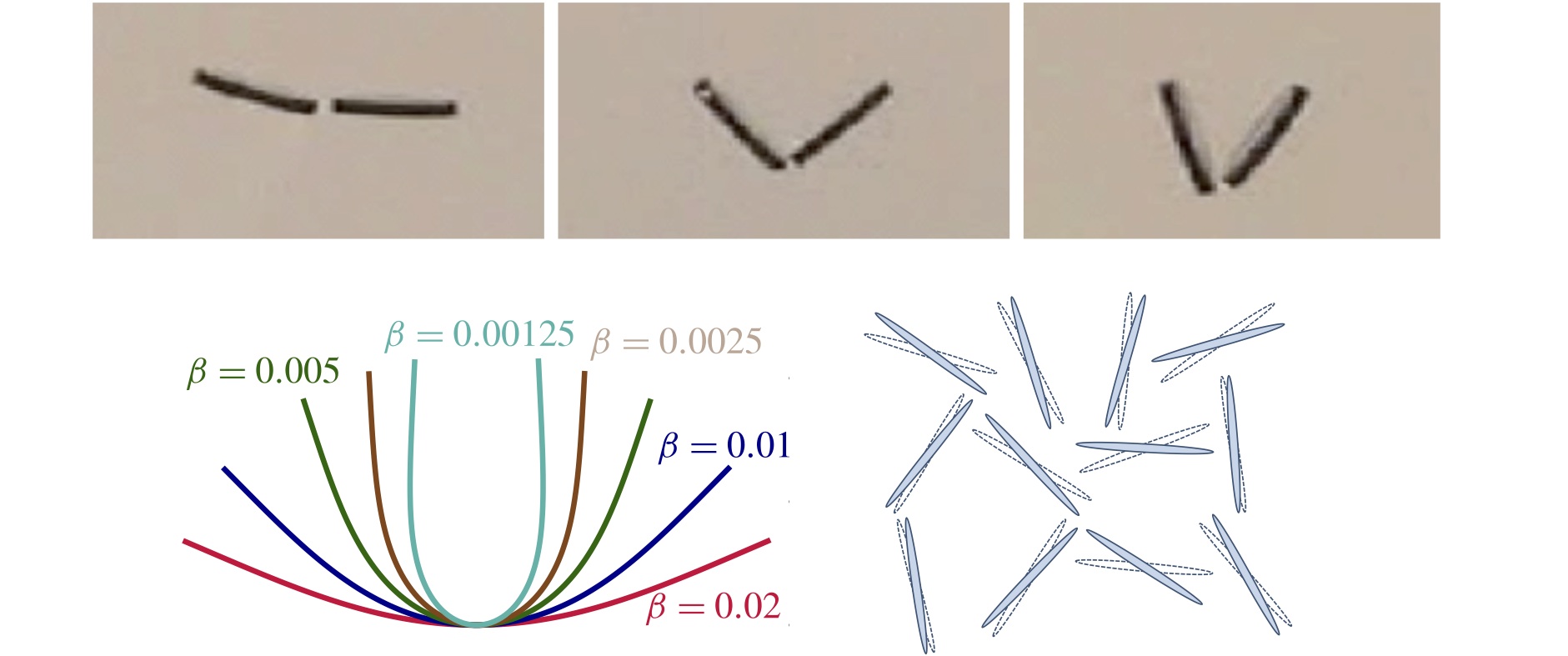
Many fundamental questions remain unanswered about the sedimentation of bodies in viscous fluids. For instance, even the dynamics of a single flexible filament have only recently been analyzed, and the interactions of viscous and elastic stresses can lead to slow shape changes or rapid buckling dynamics, as characterized by a dimensionless elasto-gravitation number. The dynamics of suspensions of flexible bodies has only just begun to receive mathematical attention, and even then only for weakly flexible filaments. Even two rigid sedimenting particles can undergo complex periodic sedimentation dynamics, so the general case is far from being completely characterized. The dynamics of flexible bodies in viscous flows remains both beautiful and analytically challenging, and is a topic of considerable practical interest.

Papers:

W. H. Mitchell and S.E. Spagnolie, A generalized traction integral equation for Stokes flow, with applications to near-wall particle mobility and viscous erosion, J. Comput. Phys., 333, 462-482 (2017).

W. H. Mitchell and S.E. Spagnolie, Sedimentation of spheroidal bodies near walls in viscous fluids: glancing, reversing, tumbling, and sliding, J. Fluid Mech., 772, 600-629 (2015).

H. Manikantan, L. Li, S.E. Spagnolie, and D. Saintillan, The instability of a sedimenting suspension of weakly flexible fibres, J. Fluid Mech., 756, 935-964 (2014).

L. Li, H. Manikantan, D. Saintillan and S.E. Spagnolie, The sedimentation of flexible filaments, J. Fluid Mech., 735, 705-736 (2013).

S.Jung, S.E. Spagnolie, K. Parikh, M. Shelley, and A-K. Tornberg, Periodic sedimentation in a Stokesian Fluid, Phys. Rev. E, 74, 035302 (2006).

Inertial fluid-body interactions

More flexible bodies in fluids...

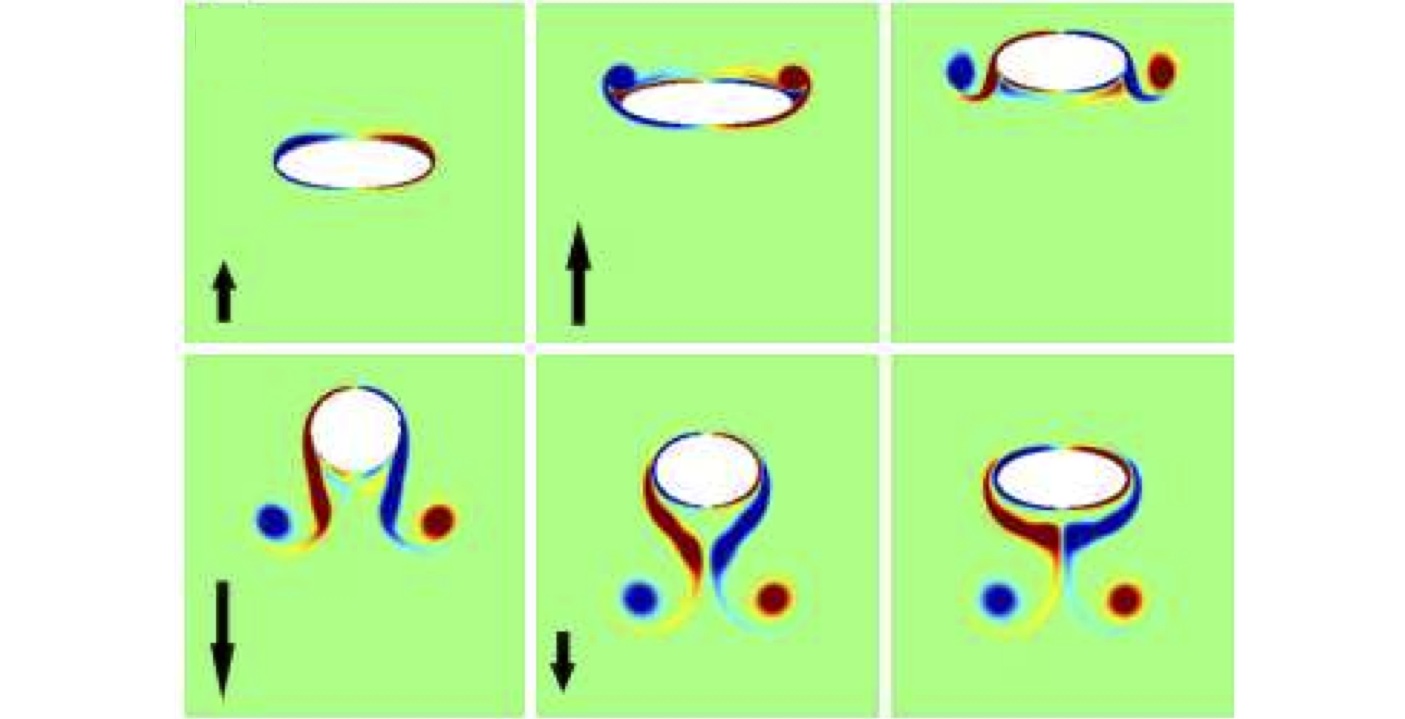
The fluid flows relevant to the swimming and flying of larger organisms, from fish to birds (or even small but fast-moving insects) are generally history-dependent and highly complex, and hence very challenging to understand mathematically. Of particular interest in the last decades have been the interaction of flapping wings/ fins with a fluid flow, thrust and lift production via vorticity generation, and the effects of flexibility on propulsion. The dynamics of shape-changing bodies in fluids is surprisingly revealing about the basic fluid-body interactions relevant to hovering and some other evasive modes of locomotion. Symmetry-breaking instabilities, interactions with previously shed vorticity, and sustained locomotion are particularly intriguing fields of active inquiry.

Papers:

T. Morrell, S.E. Spagnolie, and J.-L. Thiffeault, Velocity fluctuations in a dilute suspension of viscous vortex rings, Phys. Rev. Fluids, 4, 044501 (2019).

S. Childress, S.E. Spagnolie, and T. Tokieda, A bug on a raft: Recoil locomotion in a viscous fluid, J. Fluid Mech., 669, 527-556 (2011).

S.E. Spagnolie, L. Moret, M.J. Shelley, and J. Zhang, Surprising behaviors in flapping locomotion with passive pitching, Phys. Fluids, 22, 041903 (2010).

S.E. Spagnolie and M.J. Shelley, Shape-changing bodies in fluid: Hovering, ratcheting, and bursting, Phys. Fluids, 21, 013103 (2009).

The dynamics of flexible bodies in fluids is a research area where exciting questions abound. The interactions of body elasticity and fluid stresses can lead to filament buckling in sedimentation, shear flows, and floating systems. The time-dependent shapes taken by flexible filaments can be important for fluid rheology when the fluid contains many such bodies. Equilibrium shapes due to passive hydrodynamic and other physical effects might also be used in efforts towards self-assembly at the micro-scale.