Math 234 — Study guide 1st midterm

Syllabus  |  Homework assignments  |  About the exams  |  Using your computer  |  Lecture schedule

Topics covered

Vectors.

Vector functions/Parametric curves.

Quadratic functions.

(as in problems 5 and 6 for chapter 3.)

Extra problems

    About plane curves and tangents

  1. (a) Find a parametric equation for the line $\ell$ through the points $A (3,0,1)$ and $B (2,1,2)$.

    (b) Where does $\ell$ intersect the coordinate planes? answer

  2. (a) Find a parametric equation for the line which contains the two points $A =(2,3,1)$ and $B =(3, 2, 3 )$.

    (b) The point $C = (c_1, 1, c_3)$ is on this line. What is $C$? answer

  3. Let $A$ be the point $(1,0)$ in the plane, and let $X(t)$ be the point $(t, t^2)$.

    (a) Which curve is traced out by the point $X(t)$ as you vary the parameter $t$?

    (b) Find a parametric representation for the line $\ell$ through $A$ and $X(t)$. (since the point $X(t)$ depends on $t$, you will get a different line for each choice of $t$.)

    (c) Let $t$ be any number. Where does the line $\ell$ intersect the $y$-axis?

    answer
  4. Consider the plane curve given by $\vx(t) = \begin{pmatrix} t^2 \\ t^3 \end{pmatrix}$

    (a) Find a parametric representation of the tangent line to the curve at the point with position vector $\vx(1)$.

    (b) Find a parametric representation of the tangent line to the curve at the point with position vector $\vx(a)$ for any value of the constant $a$.

    (b) The velocity vector is still $\vx'(t) = \vek 2t \\ 3t^2 \tor$, so the velocity vector at $t=a$ is $\vx'(a) = \vek 2a\\3a^2 \tor$. This vector is a tangent vector to the curve at the point $\vx(a) = \vek a^2 \\a^3 \tor$. So the tangent at this point is the line through $\vx(a)$ with direction $\vx'(a)$: \[ \vy(t) = \vek a^2\\a^3\tor + t \vek 2a\\3a^2\tor \]

    answer

    About cross and dot products, and the product rule

  5. A vector function $\vx(t)$ describes the motion of a point in space. It is known that there is a constant vector $\vm$ such that the velocity $\vv(t)$ always satisfies $\vv(t) = \vm \times \vx(t)$. Show that the quantity $\vm\cdot \vx(t)$ is constant. answer
  6. A vector function $\vx(t)$ describes the motion of a point in space. It is known that there is a constant vector $\vm$ such that the velocity $\vv(t)$ and acceleration $\va(t)$ always satisfy $\va(t) = \vm \times \vv(t)$. Show that the quantity $\|\vv(t)\|^2$ is constant. Then show that the angle between $\vm$ and $\vv(t)$ is constant (hint: look at the dot product $\vm\cdot\vv(t)$).
  7. A vector function $\vx(t)$ describes the motion of a point in space. It is known that there is a constant number $C$ such that the acceleration $\va(t)$ always satisfies $\va(t) = -C \vx(t)$. Show that the quantity $\vx(t)\times\vv(t)$ is constant (where $\vv(t)$ is by definition the velocity vector).

Answers

Answer to Problem 1: (a) $\vx(t) = \vek 3\\ 0\\1 \tor + t \vek -1\\ 1\\1 \tor = \vek 3-t\\ t\\ 1+t \tor$.
(b) Intersection with $xy$ plane when $z=0$, i.e.\ when $t=-1$, at $(4, -1, 0)$. Intersection with $xz$ plane when $y=0$, when $t=0$, at $(3,0,1)$ (i.e.\ at $A$). Intersection with $yz$ plane when $x=0$, when $t=3$, at $(0, 3, 4)$.
Answer to Problem 2: (a) $\vec{x}(t)=\vek 2 \\ 3 \\ 1 \tor+t\vek 1 \\ -1 \\ 2 \tor$

(b) $C$ is the point $(4, 1, 5)$

Answer to Problem 3: (a) the parabola, $y=x^2$

(b) The equation that we know for a parametrization of a line, $\vx=\va+t\vv$, contains the variables $\vx$ and $t$. We can't use those variables because they were already used in the problem. So we change them to, say, $\vy$ and $s$: we get \[ \vy = \va + s\overrightarrow{AX} =\vek 1\\ 0 \tor + s \vek t-1 \\ t^2 \tor =\vek 1+s(t-1) \\ st^2 \tor. \]

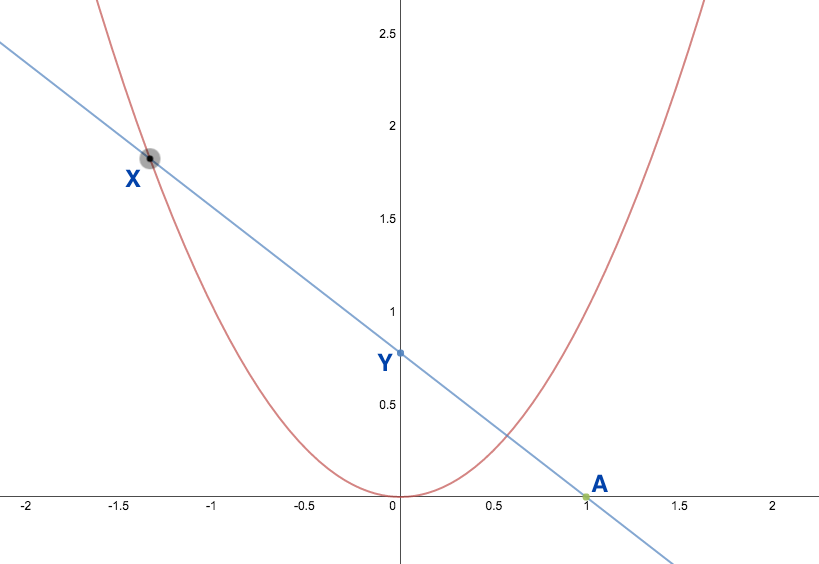
(c) What is given, and what is unknown? Here $t$ is given. Varying $s$ will slide the point $Y$ with position vector $\vy$ along the line $\ell$. So we have to find an $s$ for which $Y$ is on the $y$-axis, and, since $t$ is given, our answer will depend on $t$. The point $Y$ is on the $y$-axis if its $x$-coordinate vanishes. So, we solve \[ 1+s(t-1)=0 \implies s = \frac{1}{1-t}. \] Hence the intersection point is $Y$ with the above value of $s$ \[ \vy = \vek 0\\ t^2/(1-t) \tor. \]

Answer to problem 4:
Chapter 2, section 3, tells you how to find the parametrization of a line. Read that first before reading the rest of this answer. To parametrize a line, you need one point on the line, and a vector in the direction of the line.

(a) The velocity vector is $\vx'(t) = \vek 2t \\ 3t^2 \tor$, so the velocity vector at $t=1$ is $\vx'(1) = \vek 2\\3 \tor$. This vector is a tangent vector to the curve at the point $\vx(1) = \vek 1 \\1 \tor$. So the tangent at this point is the line through $\vx(1)$ with direction $\vx'(1)$: \[ \vy(t) = \vek 1\\1\tor + t \vek 2\\3\tor \] The $t$ in this parametrization is not the same as the $t$ in the parametrization $\vx(t)$ for the curve. To avoid confusion, one sometimes chooses a different letter, for instance, \[ \vy(s) = \vek 1\\1\tor + s \vek 2\\3\tor \] or, use a greek letter, \[ \vy(\alpha) = \vek 1\\1\tor + \alpha \vek 2\\3\tor. \]

Answer to problem 5. To show that $\vm\cdot\vx(t)$ is constant we differentiate it with respect to time, keeping in mind that the derivative $\vx'(t)$ is the same as the velocity $\vv(t)$: \[ \frac{d \vm\cdot\vx(t)} {dt} = \vm\cdot\vx'(t) = \vm\cdot\bigl(\vm\times\vx(t)\bigr). \] Since the cross product $\vm\times\vx(t)$ is always perpendicular to the vector $\vm$ it follows that \[ \frac{d \vm\cdot\vx(t)} {dt} = 0 \] so that $\vm\cdot\vx'(t)$ is indeed constant.