Math 321 homework, lecture pointers and learning objectives:
SPRING 2011
PART 2: Vector Calculus
- Homework 14, Mon. 2/21/2011 : Study Sections 1.9, 1.10 of vector notes. Vector functions, derivative, product rules
- Can you prove a product rule? any of them on page 23? Where do these products rules comes from?
- Prove the derivative of a determinant rule using index notation.
- What does a⋅da/dt=0 tell you about a? (i) if this eqn. applies at one specific time, (ii) if it applies for all times.
- What does a × da/dt=0 tell you about a? (i) if this eqn. applies at one specific time, (ii) if it applies for all times.
- Suppose you know a and da/dt. Derive expressions for d|a|/dt and
dâ/dt in terms of a and da/dt (recall that (â=a/|a|).
Do your equations say what you expect them to say? (i.e. make a sketch and interpret your results)
- If v is the velocity of a particle at position r such that
v=&omega × r, what is the acceleration a= dv/dt of the particle?
(express in the simplest, clearest way in terms of &omega and r).
What is the acceleration when &omega is a constant? Do you know what those accelerations are called?
- Consider the vector differential equation da/dt = &omega × a, where &omega is a constant vector, show that |a| and (&omega⋅a) are constants, then show that
|&omega × a| is also constant.
What is that telling you about a?
- Write dr/dt = &omega × r in index notation and
in matrix notation.
- Write dr/dt = &omega × (r-rA)
in cartesian coordinates/matrix notation.
- If da/dt = &omega x a, db/dt = &omega × b and
dc/dt = &omega × c where &omega is not necessarily constant, i.e. &omega=&omega(t),
what is d/dt [det(a, b, c)] = ? Interpret geometrically, what is going on in this problem?
(i) You should be able to derive and justify the result from your geometric understanding of the concepts without any calculations! (ii) You should also be able to derive the result using algebraic manipulations, if you know your mixed and double cross product identities. [Hint: the Jacobi identity, problem 4, section 1.5 comes in handy. ]
- Homework 15, Wed. 2/23/2011 : Study Sections 1.1, 1.2 of vector calculus notes. Curves, parametric equations.
A: ≡ A-level problem.
- Exercises: 1.2. 1, 2, 3 (largely done in class today)
- What are the canonical (or standard)
implicit and parametric equations of an ellipse? What is the parametric vector equation of an arbitrary ellipse?
(done in class, but you should be able to rederive from scratch if you understand the concepts).
A-level: Can you derive the general implicit equation of a general ellipse (say in xy space only, to make things a bit simpler).
- What is the meaning of the parameter θ (or t) in the parametric equation of an ellipse? (done in class, but do you understand it?)
- What are the canonical (or standard) implicit and parametric equations of a hyperbola? What is the general parametric equation of a hyperbola? A: Can you derive the general implicit equation of a general hyperbola (say in xy space only, to make things a bit simpler).
- Plot the ellipse and hyperbola with center C at (2,3) with a≡(3,2),|b|=2. (data given in cartesian form). Give (i) the vector parametric equations, (ii) the cartesian parametric equations, (iii) the cartesian implicit equations for those curves. Show how to derive (ii) and (iii) from (i).
- Plot the curve r=r(t) = a cos t + b sin t, where a≡(4,0) and
b≡(1,2) (in cartesian). Is this a closed curve? Find the points where r ⋅dr/dt=0
(solve in general, for arbitrary a and b). Is this an ellipse?
- What would it mean for a curve to be planar? Given an r(t), how would you check whether it corresponds to a planar curve? Is the curve r=r(t) = a + t b + t2 c planar, where
a, b and c are arbitrary constant vectors? What is the equation of the tangent line to that curve at t=1?
- Given r=r(t) = a cos t + b sin t + c, where
a, b and c are arbitrary constant vectors, except that a⋅b=0. (i) Show that the curve is planar, specify its plane. (ii) A: Find 2 fixed points r1 and r2 such that |r- r1|+ |r- r2| is a constant. Hmm, how do you formulate that problem? (and did you solve Homework 14, #5?)
- A circle is the locus of all points that are equidistant from a given point C called the center of the circle.
A similar geometric definition of an ellipse is that it is the locus of points P such that the sum of the distances
from P to two given points F1 and F2, called the foci, is a constant. This provides a
mechanical way to draw ellipses. (see Figure 10.5 in Thomas, 11th edition)
- Taking appropriate axes, show that this definition indeed corresponds to the standard algebraic equation for an ellipse.
What are the connections between the major and minor radii a, b and the geometric data?
- A+: Use the geometric definition of an ellipse to show that the lines F1P and F2P make equal angles with the tangent to the ellipse at P. Use vectors to do this in 2 lines, instead of doing it in 2 pages using coordinates. All you need is to understand tangent vector and the meaning of the position vector r=r(t) (and did you solve Homework 14, #5?)
Beautiful!
- Find a simple vector parametric equation (i.e. r=r(t))
for a curve that goes from point P1 to point P2 (in 3D space), what is the range of your t?
- Find a simple vector parametric equation for a curve that goes from points P1 to P2
and is parallel to a at P1. (hint: use products of (1-t) and t as needed with t=0 → 1. Go back to previous problem first).
- Find a simple vector parametric equation for the curve that goes from point P1 to
P2 and is parallel to a at P1 and to b at P2.
(hint: use products of (1-t) and t as needed with t=0 → 1). Got to do previous two problems before this one.
- A+: Find the vector equation for the circle that passes through points
P1, P2 and P3. Is that circle unique?
- Friday Extra: Consider the curve r=r(t) = a sec(t) + b tan(t) where sec(t)= 1/cos(t) and a⋅b=0. What kind of curve is this? Pick an a and b and sketch it for that particular a and b. Show that (sec(t))2 - (tan(t))2=1. What is r⋅a=?, r⋅b=? Try to obtain general results. What is the domain/range of t?
- Homework 16, Fri. 2/25/2011 : Study sections 1.1 and 1.2 of the
vector calc notes. You may also want to look back at your Math 222/234 book for vector functions, curves and line integrals (e.g. Thomas 11th, Chap 13 + Chap 16 for `flow integral, work and circulation')
- Concepts of curves, explicit and conceptual r=r(t) (e.g. circles and ellipses, and `connect the dots',
splines ).
- Concept of line element dr, derivative, tangent vector and line integral, study section 1.2 eqns (1), (2), (3), (4), (5), (6) and (7). Do you understand them?
- We discussed ∫C F⋅dr and a physical interpretation/application (as `Work' done by force F on a particle as it moves from point A to point B along curve C). Someone asked about the geometric meaning of ∫C r⋅dr which we computed in class. One physical interpretation for that integral is as the work done by a force F proportional to r, i.e. the force due to a spring linking the `origin' O to the point P on the curve C.
- Can you calculate the integral ∫C ra r⋅dr? where r= |r| and `a' is any real constant, e.g. a=-3 (have you ever seen that before?) or a=2, -1,...
- Can you find a meaning for the integral ∫C r |dr|? Sketch some simple but non-trivial curves and try to make sense of this integral. Heck! you can even come up with some simple explicit r(t) and actually compute that integral in that case, can't you? What is |dr|? could you think of |dr| as a constant? Can you think of dr as a constant?
- Explain why |dr| ≠ d|r| in general. Make a general sketch showing all of r, |r|, dr, |dr| and d|r|. Which ones are vectors, which ones are scalars? It is common to write |dr|=ds, and d|r|=dr. Again ds≠dr in general. s is arclength, r is distance to the origin.
- You are responsible for fully understanding eqn (7) in the notes. This is directly related to the last problem of homework 5.
- Exercises: 1.2. 4, 5, 6 (#5 done in class today for arbitrary curves!)
- Homework 17, Mon. 2/28/2011 : Study sections 1.3 and 1.4 of the vector calc notes. You may also want to look back at your Math 234 book for surfaces, surface area and surface integrals (e.g. Thomas 11th, Chap 16.5, 16.6)
- Concepts of surface, implicit (f(r)=0) and explicit parametric (r=r(u,v)) equations in vector and cartesian forms, elementary examples (planes, spheres), surface parametrizations/coordinates, coordinate curves, surface element dS.
- Exercises: 1.3. 1, 2, 3, 5
#2 is especially important,
you are expected to be able to derive all the formulas e.g. (vector) surface element dS but you are also expected to know all the relevant formulas e.g. dS = R2 sinθ dθ dφ as well as the total surface area of a sphere S = 4 π R2 and how to compute it `from scratch'. (done in class)
#5: `Outer' and `inner' radius could be interpreted in various ways. Don't run to mama (or papa, or Boyd) right away.
Digest the given formula for x,y,z to figure out the meaning of R and a, this should be fairly elementary my dear Watson! Can you explain how you deduced the meaning of R and a?
- Exercises: 1.4. 1, 2, 3, 4
- What is dS for this surface:
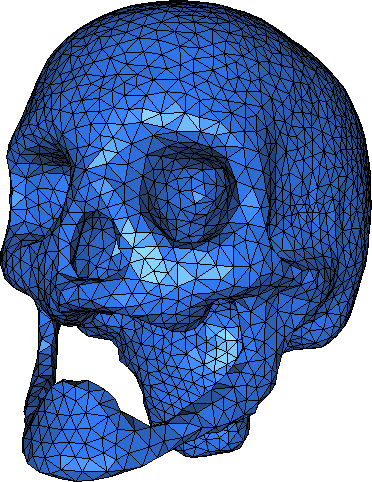 ? or
this one:
? or
this one:
 ?
How would you define the surface? How would you compute their area? How would you compute the net pressure force on the skull or the shark given a pressure field p=p(r)? (not constant pressure)
?
How would you define the surface? How would you compute their area? How would you compute the net pressure force on the skull or the shark given a pressure field p=p(r)? (not constant pressure)
- Homework 18, Wed. 3/2/2011 : Study sections 1.3 and 1.4 of the
vector calc notes.
- Homework 19, Fri. 3/4/2011 :
Study sections 1.5 and 1.6 of the vector calc notes. You may also want to look back at your Math 234 book for cylindrical and spherical coordinates
(e.g. Thomas 11th, Chap 15.6) and substitution in multiple integrals (Chap 15.7).
(EXCEPT that Thomas uses the `american mathematician' definition of spherical coords
NOT the ISO 31-11 standard notation used in physics and engineering.
See the `Conventions' paragraph on the wikipedia spherical coords page).
- Know how to derive the volume elements in cylindrical, spherical and general curvilinear coords.
- Know what it means for generalized (curvilinear) coords to be orthogonal and how that simplifies computing the volume element.
- Introduce 3D toroidal coordinates and compute the volume of a general torus. (Exercise 1.5.4)
- A surface is specified in spherical coords as r=r(θ,φ) = a sin θ, where a is an arbitrary positive constant, and θ is our usual polar angle and φ is our usual longitude.
Try to visualize it. Explain why this is a closed surface.
Compute the volume inside this closed surface.
Homework 20, Mon. 3/7/2011 : Study sections 2.1 and 2.2 of the vector calc notes
as well as the Extra notes on gradient .
You may also want to look back at your Math 234 book for contours, level sets and gradient
(e.g. Thomas 11th, Chap 14.1. 14.5).
- Consider the following surface pressure contours over the USA:
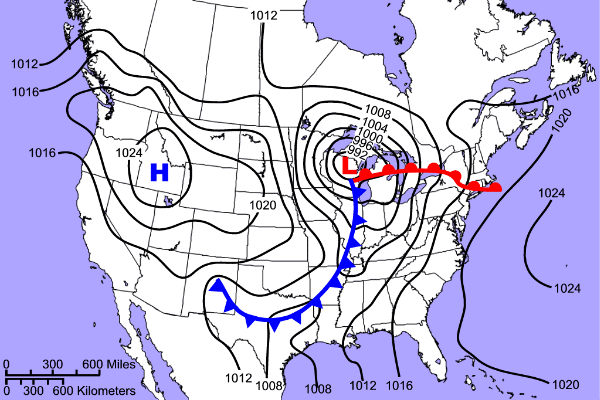 ?. Sketch the pressure gradient at (a) the south west corner of
Minnesota, (b) Madison, WI, (c) under the "H" on the figure, (d) Tallahassee, Florida. Estimate its magnitude, complete with correct units.
?. Sketch the pressure gradient at (a) the south west corner of
Minnesota, (b) Madison, WI, (c) under the "H" on the figure, (d) Tallahassee, Florida. Estimate its magnitude, complete with correct units.
- Compute the gradient of the scalar field f=f(r) for (i) f=f(|r|) ,
(ii) f=f(|r-r1|), (iii) f=f(a.r + c) where r1,
a and c are constants. Do each of these in TWO ways: (1) using your geometric understanding of the gradient, (2) using cartesian coordinates. Show that both approaches give the same result. (partially done in class)
- What is ∇f in cartesian coordinates?
- If f and g are two scalar fields, what is (i) ∇(f + g)? (ii) ∇(f g)? Why?
- From the geometric definition of an ellipse as the set of points P such that the sum of the distance
from P to two fixed points F1 and F2 is a constant, i.e.
|r-r1|+ |r-r2| = 2 a, (i) Find the direction of the normal to the ellipse at P, (ii) show that the lines (F1,P) and (F2,P) make equal angles with the normal to the ellipse at P.
- Find a function f(r) such that ∇ f = r. (partially done in class)
- Find a function f(r) such that ∇ f = r/r3. (partially done in class)
- Find a function f(r) such that ∇ f = r-r1 where r1 is a fixed position vector.
- If θ is the polar (or inclination) angle from the z axis, φ is the azimuthal (or longitude) angle from the x axis in the xy plane, ρ is the distance to the z axis, and r is the distance to the origin, find ∇r, ∇ρ, ∇φ, ∇θ. How are ∇θ and ∂r/∂θ related? How are ∇φ and ∂r/∂φ related?
(partially done in class)
- What is the general expression of the gradient of (i) f=f(x,y,z) in cartesian coords?
(ii) f=f(ρ,&phi,z) in cylindrical coords? f=f(r,θ,φ) in spherical coords?
(iv) A: f=f(q1,q2,q3) in general orthogonal coords?
(v) A+: f=f(q1,q2,q3)
in general not necessarily orthogonal coords? (cartesian and spherical done in class)
Homework 21, Wed. 3/9/2011 : Study sections 2.1 and 2.2 of the vector calc notes
as well as the Extra notes on gradient, and YOUR lecture notes. I presented things differently in class.
- What is ∇ in cartesian coords? in cylindrical coords? in spherical coords? (done in class and in these
Extra notes on gradient and
listed on this page, but can you trust everything you read on the web? You better know how to verify those formulas before using them.)
- If θ is the polar (or inclination) angle from the z axis, φ is the azimuthal (or longitude) angle from the x axis in the xy plane, ρ is the distance to the z axis, and r is the distance to the origin, express &rho, r, θ and φ in terms of cartesian coordinates.
Calculate ∇r, ∇ρ, ∇φ, ∇θ using cartesian coordinates. How else can you calculate ∇r, ∇ρ, ∇φ, ∇θ? (partially done in class)
- What is ∇ in index notation? What does ∂i mean? (done in class)
- You are responsible for understanding and knowing (60), (61), (63) in the notes. (partially done in class)
- What is a `directional derivative'? What is the derivative of f(r) at r in the direction v(r)? Give a physical example of f(r) and v(r) and explain the meaning of the derivative in question. (partially done in class)
- What is ∇⋅v in index notation? Is ∇⋅v= v⋅∇? What is the geometric meaning of v⋅∇? Compute (v⋅∇) r, for a general v, where r is the usual position vector, do that in 2 ways: (1) `geometrically' from your understanding of v⋅∇ and (2) using cartesian coords. (partially done in class)
- In index notation, what is (a) ∇× v? (b) ∇⋅(∇× v)? (c) v⋅(∇×v)? (write in index notation and try to simplify your expressions). (partially done in class)
- Is a scalar constant the same as a scalar field? Explain and give examples.
- Compute v⋅(∇ × v) for v =
α e3 + ω e3 × r,
where α and ω are scalar constants (not scalar fields, although this is mostly to make your calculations easier, they could be scalar fields) and e3 is the unit vector in the fixed z direction. Be smart, or grind it out in cartesian coords, or be ultra smart and do it both ways.
- Exercises: 2.4. 1, 7, 8, 9
- A+: What is ∇⋅v in spherical coords? well it's listed here but how do you derive/show that result?
Homework 22, Fri. 3/11/2011 : Study sections 2.3 and 2.4 of the vector calc notes
- NOTE: although we are trying to move beyond cartesian coordinates, it is OK to write expressions in cartesian coordinates to help you understand what they are. Really. It is OK. Much better than staying stuck in the "Huh?!?" state.
- We discussed: Is ∇⋅v = v⋅∇? We wrote them in cartesian coordinates. We explained what these two very different things mean.
What is ∇?
- We proved (64).
- You prove (65).
- You prove (66), (67), (68), (70) and (71).
- We calculated ∇×(r3 r) using (65) and our understanding of gradients of spherical functions which you had studied
carefully on the bottom of page 15 (`It follows immediately from our geometric understanding of gradient that ....').
- Exercises: 2.4. 1, 7, 8, 9. Grind it out in cartesian (x,y,z, etc.) if all else fails, in cartesian with rocket boosters (i.e. index notation) and/or using vector identities and intelligence. Sometimes a combination of methods is best. There is not one method that always works better.
3/21 and 3/23 EXAM 2 INTERLUDE
Homework 23, Fri. 3/25/2011 : Study section 3.2 of the
vector calc notes. That is the Fundamental Theorem of Calculus that you studied in Math 221, or earlier. Application to line integrals.
- Line integrals ∫C F⋅dr over a curv C from point A to point B in 3D space.
Examples (i) F= ra r (hwk 16, #4), (ii) F=∇f for an arbitrary scalar field f, (iii) F=∇φ where φ is the polar angle such that x=ρ cosφ and y= ρ sinφ. When is the integral from A to B path independent? What is the connection with the fundamental theorem of calculus?
- Write the vector field F=∇φ in cartesian coordinates with cartesian basis vectors.
Homework 24, Mon. 3/28/2011 : Study sections 3.1, 3.2, 3.3, 3.4 of the
vector calc notes. Fundamental Theorems of Calculus. Green's theorem, Stokes' Theorem.
- When is ∫C F⋅dr path independent? When is F= ∇ f ?
- Calculate ∫C F⋅dr for F = xy ex, and (i) C≡ (0,0) → (1,0) → (1,1), (ii) C≡ (0,0) → (0,1) → (1,1) (straight lines between the given points).
Is the integral path independent?
- Calculate ∫C F⋅dr for F = ∇φ, and (i) C≡ (0,0) → (1,0) → (1,1), (ii) C≡ (0,0) → (0,1) → (1,1). Is the integral path independent?
- Calculate ∫C F⋅dr for F = ∇ρ, and (i) C≡ (0,0) → (1,0) → (1,1), (ii) C≡ (0,0) → (0,1) → (1,1). Is the integral path independent?
- Is it common or special for a line integral ∫C F⋅dr to be path independent? Explain.
- What is the `circulation' of a vector field v around a closed loop? (for example
circulation of a velocity field in fluid dynamics
and Ampère's law in E&M (in applications, the line element dr is often written dl).
- What is Stokes' Theorem? Specify it completely in mathematical form.
- What is the connection between the circulation around a closed loop and the flux of a curl through a surface? What surface? Circulation of what? curl of what?
- Write Stokes' Theorem for a flat surface (i.e. an area) (i) in the xy plane, (ii) in the yz plane.
- Calculate the curl of ρ2 eφ without taking any derivative!
(where eφ is the unit vector in the φ direction).
(done too quickly in class 3/30, but enough for a hint?)
- Exercises: 3.7. 1, 2, 3, 4.
- Must know (86) inside out. Must know how to obtain (84) from (86), although proofwise, it goes the other way (81) ≡ (83) → (84) → (86).
Homework 25, Wed. 3/30/2011 : Study sections 3.1, 3.2, 3.3, 3.4 of the
vector calc notes. Fundamental Theorems of Calculus. Green's theorem, Stokes' Theorem.
- Write Stokes' Theorem on a blank sheet of paper in complete mathematical form, specifying all its ingredients and how they are connected. No, don't look it up and copy the formula. Write it down off the top of your head.
- Digest (87). What does it say? Do you need to memorize (87) or can you deduce it from (86)? How?
- Compute the curl of v= y ex using (87) and using (61) (two ways). Sketch the vector field. Remember that a curl is a vector field , so it should have three components.
- Compute the curl of v= y ex - x ey using (87) and using (61) (two ways). Sketch the vector field.
- Compute the curl of v= x ex - y ey using (87) and using (61) (two ways). Sketch the vector field.
- Compute the curl of v= ρa eφ, where a is a real constant,
using (87) and using vector identity (67) (≡ product rule, which you should know).[Hint: what is ∇φ?]
Sketch the vector field.
Discuss what happens at ρ=0 for different values of a.
Is ∇×v ever 0 everywhere? Write the vector field in cartesian coordinates with cartesian direction vectors.
What is eφ in cartesian coordinates with cartesian direction vectors? What is ρ in cartesian coordinates?
You can compute the curl in cartesian coordinates if you wish, to verify your results, but there are at least two better methods than that method of last resort! (of course better methods require better understanding).
Homework 26, Fri. 4/1/2011: Study sections 3.5, 3.6, 3.7 of the vector calc notes. Fundamental Theorems of Calculus. Gauss, Divergence, etc. Theorem. Pay attention to the boxed formulas. Do you understand them, do you know them?
- Write Gauss' Theorem on a blank sheet of paper in complete mathematical form, specifying all its ingredients and how they are connected. No, don't look it up and copy the formula. Write it down off the top of your head.
- Complete the following formula without just looking it up: ∫V ∂f/∂y dV = ? where V is a volume with sufficiently well behaved surface boundary, in 3D space.
- Explain what the divergence of a vector field means in `physical terms'.
- Exercises: 3.7. 5, 6, 7, 8, 9. (You can generalize 8 and 9 by considering v= ra r for any real constant a. #8 is a=0, #9 is a= -3. )
- Can you compute the divergence of v= ra r using the divergence theorem? How?
Onwards to the complex plane!
 ? or
this one:
? or
this one:
 ?
How would you define the surface? How would you compute their area? How would you compute the net pressure force on the skull or the shark given a pressure field p=p(r)? (not constant pressure)
?
How would you define the surface? How would you compute their area? How would you compute the net pressure force on the skull or the shark given a pressure field p=p(r)? (not constant pressure)
 ?
?