- What is our notation for a vector: (1) on this page and in books? (`Hint': a = a â= |a| â), (2) on the board and on paper? What is our notation for the magnitude of a vector? the direction of a vector? (we are using Gibbs notation)
- Direction vectors are also called `unit' vectors. What are the physical units of a `unit' vector? What is the length of a unit vector? in what units of length? Can you explain your answers?
- Make a `cheap' (but clean) 3D perspective sketch showing cartesian, cylindrical and spherical representations of an arbitrary vector in 3D space without just looking them up in your notes or a book.
- Write an arbitrary vector a in cartesian, cylindrical and spherical representations. You should be able to derive all the formulas `from scratch'. Understand the representations, learn to visualize properly (often by taking the appropriate orthogonal projection onto a plane like the horizontal (x, y) plane or the heading, zenith plane, a.k.a. meridional or longitudinal plane which we will call the (ρ,z) plane (i.e. (rho,z) plane)), and ... know your basic trig! Pythagoras, sine, cosine! You are expected to be able to derive all these relations from scratch in a short time and for different vectors a,b,r,v, E,B, ... and different names and definitions for the angles (e.g. longitude and polar angles, or longitude and latitude angles, or azimuthal and elevation angles, or heading and zenith=inclination angles,etc... different definitions, different formulas but same concepts). Wikipedia on spherical coordinates, etc. (pretty good today... also contains cylindrical coords)
- What is the vector equation that expresses the equality between the cartesian, cylindrical and spherical representation of a vector a? Deduce all algebraic relations between the various representations (i.e. cartesian and cylindrical, cylindrical and spherical, cartesian and spherical). Write the direction vectors for a and its horizontal component aH in terms of the cartesian direction vectors. What are the cartesian direction vectors? How do we write them?
- What are the cylindrical and spherical components for the vectors whose cartesian components are (0,0,1), (0,-1,0), (1,1,1)? What are the angles φ and θ for those vectors?
- If we want a unique set of components for a vector a in 3D space, what range of values do we need for (1) (ax,ay,az), (2) (aH, φ, az), (3) (a, θ, φ) ?
- (1) Express aH and a in terms of ax,ay,az. (2) Express ax,ay,az in terms of the cylindrical components aH, φ,az. (3) Express ax,ay,az in terms of spherical components a, θ, φ. You are expected to be able to rederive all these formulas from scratch, in a short time, without just regurgitating formulas.
- Express the direction vectors in the directions aH and a (that is `aH-hat', âH, and `a-hat', â) in terms of the cartesian direction vectors.
- Study sections 1.1 and 1.2 in the Vector notes . You can but are not required to try out the exercises in section 1.1, these are more Math 340 type exercises. They will not show up on the exams, but you are responsible for the content of section 1.1.
- OK, you understand how to add vectors in 3D space, but how do you subtract vectors?
Pick 2 arbitrary vectors a and b, make sketches showing a+b and a-b. Learn to quickly recognize/reconstruct a+b and a-b.
Use vector methods to show that the diagonals of a parallelogram intersect at their midpoint. - What is a vector basis? Is a basis vector a unit vector? Are basis vectors perpendicular to each other? Are basis vectors parallel to each other?
- Exercises: 1.2. 1 , 5, 6, 7, 8. (In 1.2.1(i) both α and β are between 0 and 1)
-
- Given a point A and a vector a (e.g. A= Tower of Dane County Regional airport, a = 3 miles heading 035°) (1) what is the vector equation of the line through A in the direction a? (2) What is the cartesian equation of the line if A is given in cartesian coordinates as (A1,A2,A3) and a is (a1,a2,a3)?
- An airplane moves at constant velocity v and was at position r0 at time t0. What is the vector equation of its trajectory?
- An airplane was at position r1 at some time and at r2 at another time (earlier or later, we don't know). What is the (vector) equation of its trajectory, assuming that it is moving at constant velocity?
- An airplane was at a displacement a (e.g. 2 miles heading 035°) from airport A (say Madison) at some time and at displacement b from Airport B (say Milwaukee) at another time. What is the (vector) equation of its trajectory, assuming that it has been moving at constant velocity?
- Given two vectors a and b, what is the vector component of a parallel to b? what is the vector component of a perpendicular to b? (Before saying `huh?! Boyd help me!!', did you study the notes?)
- Exercises: 1.3. 1, 2, 3, 7, 8, 9
- You know the (non zero) lengths a1, a2, a3 of three vectors a1, a2, a3, respectively. You also know the angle α1 between a2 and a3, the angle α2 between a3 and a1, and the angle α3 between a1 and a2. (1) What conditions must the angles satisfy for the vectors to be linearly independent? (2) Assume those conditions are satisfied, and that 2 vectors u and v are given to you in terms of the basis a1, a2, a3, that is u = u1a1 + u2a2 + u3a3 and v = v1a1 + v2a2 + v3a3 with (u1,u2,u3) and (v1,v2,v3) known. Express the dot product u.v in terms of the known data (derive a formula).
- Given three point A, B, C in 3D space, use vectors to find the intersection of the 3 heights (these are the lines passing through one vertex, perpendicular to the opposite side). Write an algorithm to find the intersection, i.e. a pseudo computer program. You can assume that the points are specified in cartesian coordinates.
- What is the vector equation of the plane perpendicular to direction a, passing through point A? Formulate a vector equation then spell it out in good old cartesian coords. How would you specify explicit data for a and A?
- Understand and learn formula (14) and (15). Looks easy but they are likely to come back and bite you if you try to memorize them without understanding them.
- Exercises: 1.4. 1, 2, 3, 4, 5: indices, sigma notation, dummy/summation indices
- Consider 3 points A, B, C lying on a circle. If AB is a diameter of that circle use vectors to show that the angle ACB is a right angle. (Hint: try not to use the hint later below! PS: You should be able to show this using high school geometry, can you?)
- Solve problem 4, part (2) in homework 3 using sigma notation.
- As a follow up to questions/statements in class: Take problem 4 in homework 3. What is the volume of the parallelepiped with sides a1, a2, a3? Derive a formula in terms of a1, a2, a3 and the angles α1, α2, α3. Example a1=3, a2=4, a3=5 and α1=π/3, α2=π/4, α3=π/5. [Hint: use section 1.4! but how?...]
- (`Hint-later-below': let O be the middle of AB (surprise, surprise...), then use vectors OA,OB,OC and compute a certain dot product).
- Construct an explicit simple example of 3 vectors a, b, c with components ai, i =1,2,3 in one orthonormal basis, and a'i in another orthonormal basis, and likewise for b and c to verify that aibi ( ≡ a1b1 + a2b2 + a3b3, in Einstein summation convention ) is invariant, but that a1b1c1 + a2b2c2 + a3b3c3 is not.
- Do you know formula (25)? Can you prove them? You should, you're responsible for them!
- Exercises: 1.5. 1, 2, 3, 4, 5, 6, 8
- Consider an arbitrary tetrahedron in 3D space. Label the vertices A, B, C and D in such a way that the vectors AB, AC and AD are left handed. This can always be done, right? Now define 4 area vectors, one for each face of the tetrahedron,
such that the magnitude of an area vector is equal to the triangular area of the face and its direction perpendicular to that face pointing out of the tetrahedron . Prove that the sum of those 4 area vectors is zero, for any tetrahedron.
What if you glue two tetrahedra together along a common triangular face? you get a polyhedron with 8-2 = 6 triangular faces. What is the sum of the 6 outward area vectors? What if you keep on gluing tetrahedra? What if you take any polyhedron and divide each of its faces into triangles? - The area of the triangle P1, P2, P3 is given by the magnitude of
1/2 vec(P1P2) x vec(P1P3) (right?). If O is any point in the same plane, show geometrically and algebraically that the area is also given by the magnitude of 1/2 vec(OP1) x vec(OP2) +
1/2 vec(OP2) x vec(OP3) + 1/2 vec(OP3) x vec(OP1). Is that true also if O is NOT in the same plane?
If (x1, y1), (x2, y2), (x3, y3), are the cartesian coordinates of three arbitrary points in the xy plane, prove that the area of the triangle that they form is +/- 1/2 of (x1 y2-x2 y1) + (x2 y3-x3 y2) + (x3 y1-x1 y3) . Discuss the meaning of the sign. What if you `glue' triangles together? Could you derive a formula for the area of an arbitrary planar n-gon?
- For Sean and all his friends (and he has many!): Are the two formula in (25) equal to each other or not? That is, shouldn't we have (a × b) × c = a × (b × c)? We showed in section 1.5, page (11) that the cross product was distributive with respect to vector addition: (a + b) × c = (a × c) + (b × c ), and we also have associativity of vector addition: (a + b) + c = a + (b + c) on page (2), but do we have associativity of cross product?
- Is (a × b) × c =(a × c) × (b × c) ?
- When is (a × b) × c = a × (b × c)?
- Show from the geometric definition of the cross product that (a × b) × a = a × (b × a) = a2 b⊥. State what a2 and b⊥ are in terms of a and b.
- BAC CAB rule anyone? Explain why the bac cab rule is a confusing trap. (The guy who invented it is still laughing in the back of his cab!).
- Study all of section 1.6 carefully. Read, think, understand.
- Assume a,b,c are distinct elements. What is an odd permutation of (a,b,c)? What is an even permutation of (a,b,c)? How many permutations of (a,b,c) are there?
- Prove that the number of permutations of n distinct elements is n! defined recursively as 1!=1 and n!=n × (n-1)!. Reminder and further info about the factorial of a number .
- What is a cyclic permutation of (a,b,c)? How many cyclic permutations of (a,b,c) are there?
- What is a cyclic permutation of (a,b,c,d)? How many cyclic permutations of (a,b,c,d) are there? How many even permutations of (a,b,c,d) are there?
- What is that weird inverted 3 called?
- What is εijk? What is ε231=? Is it true that εijk= εkij for any i,j,k? why? Is it true that εijk = - εkji, for any i,j,k? why?
- What does formula (28) tell us?
- Why does (28) imply (29) and vice versa?
- Why does (33) have 4 ='s then one ≠ ??!
- What is ``WRONG!'' about (35)?
- Which of the problems above did you find most interesting?
- Study section 1.6, don't just skip it and go straight to the exercises or the TA. Study every line, every expression, every equation. Does this mean you should memorize everything?!? What does it mean to study equation (38) for instance?
- Study (39) and write it with other indices. Why is it boxed? is it to pack it away in the attic and forget about it?
- The derivation from (40) to (44) was done in class, although probably with other indices.
- Write a×b, (a×b)m, (a×b) ⋅ en, ei ⋅ (a×b), (a×b) ×c, ((a×b) ×c)m and ((a×b) ×c) .ei in index notation using Einstein's summation convention.
- Evaluate εijk εijl
- True or False: εijk ai bj + εklm am bl = 0. WHY?
- Study (44).
- Deduce (44) from (45).
- Exercises: 1.7. 1, 2, 3, 7, 8, 9, 10, 11, 12
- Write exercises 11 and 12 in index notation with the summation convention. (Exercises 11 and 12 are 2 different versions of the same problem, do you see that?).
- Solve all the problems in section 1.8.
- Note: you should have seen all of this in Calc 2, e.g. Thomas 11th edition, section 12.5 Lines and Planes in space.
- Lecture started with a little talk about determinants in ℝ2 and ℝ3 and how they correspond to signed areas in 2D and signed volumes in 3D. We took a peek at determinants in ℝn and the Leibniz formula for determinants, although that's beyond Math 321.
- Solve all the problems in section 1.8.
- Compare equations (63) with exercise 1.5.3.
- Compare equations (64) with exercise 1.3.2.
- Answer these questions, and these too. These are `real world' problems. Since the real world is full of people who don't quite know what they are talking about, you first need to decypher the confused questions to make sense of them.
- If the primed basis is the same as the unprimed basis except that e'1=-e1, what is the matrix Q such that v'i=Qijvj?
- If the primed basis corresponds to a rotation of the unprimed basis about the e2 direction by angle β what is the matrix Q such that v'i=Qijvj?
- If any two sets of cartesian components are related by v'i=Qijvj? What is the determinant of Q? Does your answer match the two previous specific examples?
- If (v1,v2,v3), (v'1,v'2,v'3) and (v''1,v''2,v''3) are the components of a vector v with respect to three distinct orthonormal bases (i.e. cartesian bases if you wish), and v'i=Aijvj, v''i=Bijv'j, (1) what is AklAkm=?, (2) if v''i = Cijvj, what is Cij=? in terms of the A's and B's, (3) what is CijCik=?, (4) what is CijCkj=? Can you prove/explain/justify your answers?
- The unprimed basis (e1, e2, e3 ) corresponds to cartesian coordinates centered at the center of the earth, with the x direction corresponding to longitude 0, latitude 0 and the z axis as the polar axis. The primed basis (e'1, e'2, e'3 ) corresponds to cartesian coordinates centered at Madison, WI, with the z' axis vertical and the x' axis pointing east. Both systems are right handed. If a vector v has components (v1,v2,v3) in the earth basis, what are its components in the Madison basis? If a point has cartesian coordinates (x1,x2,x3) in the earth basis, what are its coordinates in the Madison basis? Madison, WI is at 43° 4' 23" N, 89° 24' 4" W (Of course, you need a good understanding of Lecture 1, spherical, cylindrical and cartesian representations of vectors to solve this problem. Don't make a `bouillabaisse' of numbers right away. Formulate the problem for arbitrary longitude φ and latitude λ first. In other words, derive the general procedure that we could use for a San Diego basis, or New York or Bermuda! not just Madison).
- Euler angles Take a look at that wikipedia page and don't get scared. The first figure is what we did in class today. The wikipedia page refers to that definition as Z-X'-Z''. You should understand what that means since that is what we did today. Look at the applications at the bottom of the page. Basically, these concepts are useful to any engineer or scientist who has to describe/control 3D objects in 3D space. Even quantum mechanicians and molecular biologists.
- You should understand what this is about:
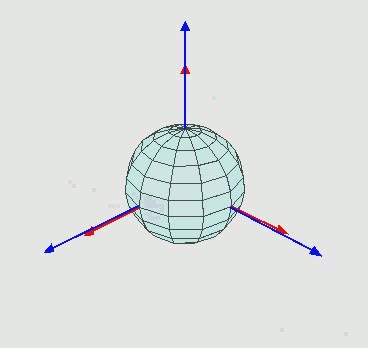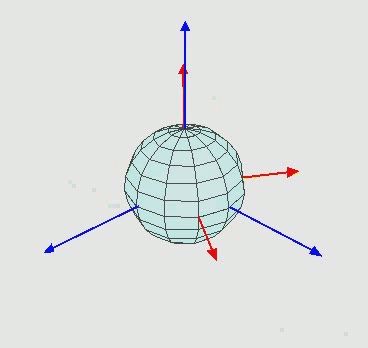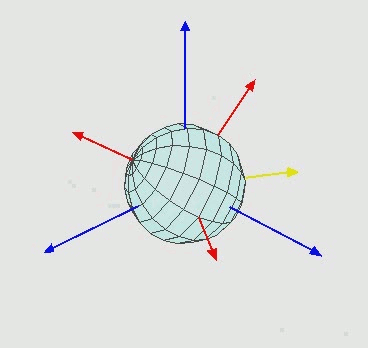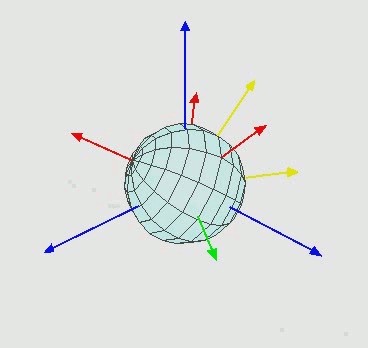That's what we did in class today.
- What would eqn (95) correspond to? (Hint: Z-Y'-Z'', explain).
- Solve problem 5 of homework 11 using 3 elementary transformations.
- For those of you who wish you were given all the answers (and paid for it too?!), note that we effectively solved in class today alternative versions of problems 2 and 4 of homework 11.
- Want to know more?
- Axes conventions
- Gyroscope
- Gyroscope on the iPhone 4
- Gyroscope in Wii
- Gimbal (no, not "Gym Ball")
- Gimbal Lock
- Yaw, Pitch, Roll
- We spent most of the lecture answering the question: what is Qij Qjk? That was a great question! We started with a simple but non-trivial example for Q, then noticed something `obvious' about the result of our example. `Obvious' if we ground through the trig correctly then looked carefully at our result (not the route I took), or stopped and thought about what we were doing (i.e. two successive identical rotations) and checked it with the trig to make sure we were not delusional. Then we tried to verify it in general, for any orthogonal matrix Q, using index notation.
- Optional: Develop an `App' for the iPhone4 that makes use of its gyroscope (I claim 10% or your profits!).
- FYI, two companies that make MEMS gyros: InvenSense and Analog Devices (I'm not recommending that you buy anything, just informing you about modern tech industries where they make devices that use Euler angles or related concepts, and how these are hidden into your iPhone4 or your Wii or your ...)
- I suspect that (as is often the case) many students are trying to tackle the exercises directly, by trial and error and a lot of help from the TA, without first digesting the notes and the concepts. For instance, it seems that few have actually digested the last 2 equations on the bottom of page (29). You have been told that result many times in the lectures and how they explain/imply (88) and (89), but can you actually deduce all of it for yourself? Yep, we've got two sets of three orthonormal vectors, so this is not trivial, but it can be understood. The cool thing about true understanding is that suddenly it all makes sense and you `know' all the formulas.