REVIEW¶
Spectral theorem¶
Course: Math 833 - Modern Discrete Probability (MDP)
Author: Sebastien Roch, Department of Mathematics, University of Wisconsin-Madison
Updated: Nov 20, 2020
Copyright: © 2020 Sebastien Roch
1 Statement and proof of the spectral theorem¶
When $A$ is symmetric, that is, $a_{ij} = a_{ji}$ for all $i,j$, a remarkable result is that $A$ is similar to a diagonal matrix by an orthogonal transformation. Put differently, there exits an orthonormal basis of $\mathbb{R}^d$ made of eigenvectors of $A$.
Theorem (Spectral Theorem): Let $A \in \mathbb{R}^{d \times d}$ be a symmetric matrix, that is, $A^T = A$. Then $A$ has $d$ orthonormal eigenvectors $\mathbf{q}_1, \ldots, \mathbf{q}_d$ with corresponding (not necessarily distinct) real eigenvalues $\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_d$. In matrix form, this is written as the matrix factorization
$$ A = Q \Lambda Q^T = \sum_{i=1}^d \lambda_i \mathbf{q}_i \mathbf{q}_i^T $$where $Q$ has columns $\mathbf{q}_1, \ldots, \mathbf{q}_d$ and $\Lambda = \mathrm{diag}(\lambda_1, \ldots, \lambda_d)$. We refer to this factorization as a spectral decomposition of $A$.
Proof idea (Spectral Theorem): Use a greedy sequence maximizing the quadratic form $\langle \mathbf{v}, A \mathbf{v}\rangle$. How is this quadratic form is related to eigenvalues? Note that, for a unit eigenvector $\mathbf{v}$ with eigenvalue $\lambda$, we have $\langle \mathbf{v}, A \mathbf{v}\rangle = \langle \mathbf{v}, \lambda \mathbf{v}\rangle = \lambda$.
Exercise: Consider the block matrices
$$ \begin{pmatrix} \mathbf{y}\\ \mathbf{z} \end{pmatrix} \quad \text{and} \quad \begin{pmatrix} A & B\\ C & D \end{pmatrix} $$where $\mathbf{y}\in\mathbb{R}^{d_1}$, $\mathbf{z}\in\mathbb{R}^{d_2}$, $A \in \mathbb{R}^{d_1 \times d_1}$, $B \in \mathbb{R}^{d_1 \times d_2}$, $C \in \mathbb{R}^{d_2 \times d_1}$, and $D \in \mathbb{R}^{d_2 \times d_2}$. Show that
$$ \begin{pmatrix} \mathbf{y}\\ \mathbf{z} \end{pmatrix}^T \begin{pmatrix} A & B\\ C & D \end{pmatrix} \begin{pmatrix} \mathbf{y}\\ \mathbf{z} \end{pmatrix} = \mathbf{y}^T A \mathbf{y} + \mathbf{y}^T B \mathbf{z} + \mathbf{z}^T C \mathbf{y} + \mathbf{z}^T D \mathbf{z}. $$$\lhd$
Proof (Spectral Theorem): We proceed by induction.
A first eigenvector: Let $A_1 = A$ and
$$ \mathbf{v}_1 \in \arg\max\{\langle \mathbf{v}, A_1 \mathbf{v}\rangle:\|\mathbf{v}\| = 1\} $$and
$$ \lambda_1 = \max\{\langle \mathbf{v}, A_1 \mathbf{v}\rangle:\|\mathbf{v}\| = 1\}. $$Complete $\mathbf{v}_1$ into an orthonormal basis of $\mathbb{R}^d$, $\mathbf{v}_1$, $\hat{\mathbf{v}}_2, \ldots, \hat{\mathbf{v}}_d$, and form the block matrix
$$ \hat{W}_1 = \begin{pmatrix} \mathbf{v}_1 & \hat{V}_1 \end{pmatrix} $$where the columns of $\hat{V}_1$ are $\hat{\mathbf{v}}_2, \ldots, \hat{\mathbf{v}}_d$. Note that $\hat{W}_1$ is orthogonal by construction.
Getting one step closer to diagonalization: We show next that $W_1$ gets us one step closer to a diagonal matrix by similarity transformation. Note first that
$$ \hat{W}_1^T A_1 \hat{W}_1 = \begin{pmatrix} \lambda_1 & \mathbf{w}_1^T \\ \mathbf{w}_1 & A_2 \end{pmatrix} $$where $\mathbf{w}_1 = \hat{V}_1^T A_1 \mathbf{v}_1$ and $A_2 = \hat{V}_1^T A_1 \hat{V}_1$. The key claim is that $\mathbf{w}_1 = \mathbf{0}$. This follows from a contradiction argument.
Indeed, suppose $\mathbf{w}_1 \neq \mathbf{0}$ and consider the unit vector
$$ \mathbf{z} = \hat{W}_1 \times \frac{1}{\sqrt{1 + \delta^2 \|\mathbf{w}_1\|^2}} \begin{pmatrix} 1 \\ \delta \mathbf{w}_1 \end{pmatrix} $$which, by the exercise above, achieves objective value
$$ \begin{align*} \mathbf{z}^T A_1 \mathbf{z} &= \frac{1}{1 + \delta^2 \|\mathbf{w}_1\|^2} \begin{pmatrix} 1 \\ \delta \mathbf{w}_1 \end{pmatrix}^T \begin{pmatrix} \lambda_1 & \mathbf{w}_1^T \\ \mathbf{w}_1 & A_2 \end{pmatrix} \begin{pmatrix} 1 \\ \delta \mathbf{w}_1 \end{pmatrix}\\ &= \frac{1}{1 + \delta^2 \|\mathbf{w}_1\|^2} \left( \lambda_1 + 2 \delta \|\mathbf{w}_1\|^2 + \delta^2 \mathbf{w}_1^T A_2 \mathbf{w}_1 \right). \end{align*} $$By a Taylor expansion, for $\epsilon \in (0,1)$ small,
$$ \frac{1}{\sqrt{1 + \epsilon^2}} \approx 1 - \epsilon^2/2. $$So, for $\delta$ small,
$$ \begin{align} \mathbf{z}^T A_1 \mathbf{z} &\approx (\lambda_1 + 2 \delta \|\mathbf{w}_1\|^2 + \delta^2 \mathbf{w}_1^T A_2 \mathbf{w}_1) (1 - \delta^2 \|\mathbf{w}_1\|^2/2)\\ &\approx \lambda_1 + 2 \delta \|\mathbf{w}_1\|^2 + C \delta^2\\ &> \lambda_1 \end{align} $$where $C \in \mathbb{R}$ depends on $\mathbf{w}_1$ and $A_2$. That gives the desired contradiction.
So, letting $W_1 = \hat{W}_1$,
$$ W_1^T A_1 W_1 = \begin{pmatrix} \lambda_1 & \mathbf{0} \\ \mathbf{0} & A_2 \end{pmatrix}. $$Finally note that $A_2 = \hat{V}_1^T A_1 \hat{V}_1$ is symmetric
$$ A_2^T = (\hat{V}_1^T A_1 \hat{V}_1)^T = \hat{V}_1^T A_1^T \hat{V}_1 = \hat{V}_1^T A_1 \hat{V}_1 = A_2 $$by the symmetry of $A_1$ itself.
Next step of the induction: Apply the same argument to the symmetric matrix $A_2 \in \mathbb{R}^{(d-1)\times (d-1)}$, let $\hat{W}_2 \in \mathbb{R}^{(d-1)\times (d-1)}$ be the corresponding orthogonal matrix, and define $\lambda_2$ and $A_3$ through the equation
$$ \hat{W}_2^T A_2 \hat{W}_2 = \begin{pmatrix} \lambda_2 & \mathbf{0} \\ \mathbf{0} & A_3 \end{pmatrix}. $$Define the block matrix
$$ W_2 = \begin{pmatrix} 1 & \mathbf{0}\\ \mathbf{0} & \hat{W}_2 \end{pmatrix} $$and observe that
$$ W_2^T W_1^T A_1 W_1 W_2 = W_2^T \begin{pmatrix} \lambda_1 & \mathbf{0} \\ \mathbf{0} & A_2 \end{pmatrix} W_2 = \begin{pmatrix} \lambda_1 & \mathbf{0}\\ \mathbf{0} & \hat{W}_2^T A_2 \hat{W}_2 \end{pmatrix} =\begin{pmatrix} \lambda_1 & 0 & \mathbf{0} \\ 0 & \lambda_2 & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & A_3 \end{pmatrix}. $$Proceeding similarly by induction gives the claim. $\square$
2 Extremal characterization of eigenvalues¶
We derive an important extremal characterization inspired by the proof of the spectral theorem. We will need the following notion, which appeared already in the proof.
Definition (Rayleigh Quotient): Let $A \in \mathbb{R}^{d \times d}$ be a symmetric matrix. The Rayleigh quotient is defined as
$$ \mathcal{R}_A(\mathbf{u}) = \frac{\langle \mathbf{u}, A \mathbf{u} \rangle}{\langle \mathbf{u}, \mathbf{u} \rangle} $$which is defined for any $\mathbf{u} \neq \mathbf{0}$ in $\mathbb{R}^{d}$. $\lhd$
Exercise: Let $A \in \mathbb{R}^{d \times d}$ be a symmetric matrix. Let $\mathbf{v}$ be a (not necessarily unit) eigenvector of $A$ with eigenvalue $\lambda$. Show that $\mathcal{R}_A(\mathbf{v}) = \lambda$. $\lhd$
Exercise: Let $\mathcal{U}, \mathcal{V} \subseteq \mathbb{R}^d$ be subspaces such that $\mathrm{dim}(\mathcal{U}) + \mathrm{dim}(\mathcal{V}) > d$. Show there exists a non-zero vector in the intersection $\mathcal{U} \cap \mathcal{V}$. [Hint: Take the union of a basis for $\mathcal{U}$ and a basis for $\mathcal{V}$, then use linear dependence.] $\lhd$
Theorem (Courant-Fischer): Let $A \in \mathbb{R}^{d \times d}$ be a symmetric matrix with spectral decomposition $A = \sum_{i=1}^d \lambda_i \mathbf{v}_i \mathbf{v}_i^T$ where $\lambda_1 \geq \cdots \geq \lambda_d$. For each $k = 1,\ldots,d$, define the subspace
$$ \mathcal{V}_k = \mathrm{span}(\mathbf{v}_1, \ldots, \mathbf{v}_k) \quad\text{and}\quad \mathcal{W}_{d-k+1} = \mathrm{span}(\mathbf{v}_k, \ldots, \mathbf{v}_d). $$Then, for all $k = 1,\ldots,d$,
$$ \lambda_k = \min_{\mathbf{u} \in \mathcal{V}_k} \mathcal{R}_A(\mathbf{u}) = \max_{\mathbf{u} \in \mathcal{W}_{d-k+1}} \mathcal{R}_A(\mathbf{u}). $$Furthermore we have the following min-max formulas, which do not depend on the choice of spectral decomposition, for all $k = 1,\ldots,d$
$$ \lambda_k = \max_{\mathrm{dim}(\mathcal{V}) = k} \min_{\mathbf{u} \in \mathcal{V}} \mathcal{R}_A(\mathbf{u}) = \min_{\mathrm{dim}(\mathcal{W}) = d-k+1} \max_{\mathbf{u} \in \mathcal{W}} \mathcal{R}_A(\mathbf{u}). $$Proof idea: For the local formula, we expand a vector in $\mathcal{V}_k$ into the basis $\mathbf{v}_1,\ldots,\mathbf{v}_k$ and use the fact that $\mathcal{R}_A(\mathbf{v}_i) = \lambda_i$ and that eigenvalues are in non-increasing order. The global formulas then follow from a dimension argument.
Proof: We first prove the local formula, that is, the one involving a specific decomposition.
Local formulas: Since $\mathbf{v}_1, \ldots, \mathbf{v}_k$ form an orthonormal basis of $\mathcal{V}_k$, any nonzero vector $\mathbf{u} \in \mathcal{V}_k$ can be written as $\mathbf{u} = \sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle \mathbf{v}_i$ and it follows that
$$ \langle \mathbf{u}, \mathbf{u} \rangle = \sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle^2 $$$$ \langle \mathbf{u}, A \mathbf{u} \rangle = \left\langle \mathbf{u}, \sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle \lambda_i \mathbf{v}_i \right\rangle = \sum_{i=1}^k \lambda_i \langle \mathbf{u}, \mathbf{v}_i \rangle^2. $$Thus,
$$ \mathcal{R}_A(\mathbf{u}) = \frac{\langle \mathbf{u}, A \mathbf{u} \rangle}{\langle \mathbf{u}, \mathbf{u} \rangle} = \frac{\sum_{i=1}^k \lambda_i \langle \mathbf{u}, \mathbf{v}_i \rangle^2}{\sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle^2} \geq \lambda_k \frac{\sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle^2}{\sum_{i=1}^k \langle \mathbf{u}, \mathbf{v}_i \rangle^2} = \lambda_k $$where we used $\lambda_1 \geq \cdots \geq \lambda_k$ and the fact that $\langle \mathbf{u}, \mathbf{v}_i \rangle^2 \geq 0$. Moreover $\mathcal{R}_A(\mathbf{v}_k) = \lambda_k$. So we have established
$$ \lambda_k = \min_{\mathbf{u} \in \mathcal{V}_k} \mathcal{R}_A(\mathbf{u}). $$The expression in terms of $\mathcal{W}_{d-k+1}$ is proved similarly.
Global formulas: Since $\mathcal{V}_k$ has dimension $k$, it follows from the local formula that
$$ \lambda_k = \min_{\mathbf{u} \in \mathcal{V}_k} \mathcal{R}_A(\mathbf{u}) \leq \max_{\mathrm{dim}(\mathcal{V}) = k} \min_{\mathbf{u} \in \mathcal{V}} \mathcal{R}_A(\mathbf{u}). $$Let $\mathcal{V}$ be any subspace with dimension $k$. Because $\mathcal{W}_{d-k+1}$ has dimension $d - k + 1$, we have that $\dim(\mathcal{V}) + \mathrm{dim}(\mathcal{W}_{d-k+1}) > d$ and there must be non-zero vector $\mathbf{u}_0$ in the intersection $\mathcal{V} \cap \mathcal{W}_{d-k+1}$ by the exercise above.
We then have by the other local formula that
$$ \lambda_k = \max_{\mathbf{u} \in \mathcal{W}_{d-k+1}} \mathcal{R}_A(\mathbf{u}) \geq \mathcal{R}_A(\mathbf{u}_0) \geq \min_{\mathbf{u} \in \mathcal{V}} \mathcal{R}_A(\mathbf{u}). $$Since this inequality holds for any subspace of dimension $k$, we have
$$ \lambda_k \geq \max_{\mathrm{dim}(\mathcal{V}) = k} \min_{\mathbf{u} \in \mathcal{V}} \mathcal{R}_A(\mathbf{u}). $$Combining with inequality in the other direction above gives the claim. The other global formula is proved similarly. $\square$
3 Application to spectral graph theory¶
We give a quick application of the extremal characterization of eigenvalues to spectral graph theory.
3.1 Matrices associated to graphs¶
A convenient way of specifying a graph is the following matrix representation.
Definition (Adjacency Matrix): Assume the undirected graph $G = (V,E)$ has $n = |V|$ vertices. The adjacency matrix $A$ of $G$ is the $n\times n$ symmetric matrix defined as
$$ \begin{align} A_{xy} = \begin{cases} 1 & \text{if $\{x,y\} \in E$}\\ 0 & \text{o.w.} \end{cases} \end{align} $$$\lhd$
Example (Triangle): The adjacency matrix of a triangle:

(Source)
that is, $3$ vertices with all possible edges between them, is
$\lhd$
Exercise: Let $A^n$ be the $n$-th matrix power of the adjacency matrix $A$ of a graph $G = (V, E)$. Prove that the $(i,j)$-th entry $a^n_{ij}$ is the number of paths of length exactly $n$ between vertices $i$ and $j$ in $G$. (Hint: Use induction on $n$.) $\lhd$
Another useful matrix associated to a graph is its incidence matrix. For convenience, we assume that the vertices of $G = (V,E)$ are numbered $1, \ldots, |V|$ and that the edges are labeled arbitrarily as $e_1, \ldots, e_|E|$.
Definition (Incidence Matrix): The incidence matrix of an undirected graph $G = (V, E)$ is the $n \times m$ matrix $B$, where $n = |V|$ and $m =|E|$ are the numbers of vertices and edges respectively, such that $B_{ij} = 1$ if the vertex $i$ and edge $e_j$ are incident and 0 otherwise. $\lhd$
Example: The incidence matrix of the following graph:
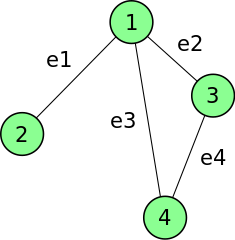
(Source)
is given by
$\lhd$
In the digraph case, we have the definitions are adapted as follows. The adjacency matrix $A$ of a digraph $G = (V, E)$ is the matrix defined as
$$ \begin{align} A_{xy} = \begin{cases} 1 & \text{if $(x,y) \in E$}\\ 0 & \text{o.w.} \end{cases} \end{align} $$The oriented incidence matrix of a digraph $G$ with vertices $1,\ldots,n$ and edges $e_1, \ldots, e_m$ is the matrix $B$ such that $B_{ij} = -1$ if egde $e_j$ leaves vertex $i$, $B_{ij} = 1$ if egde $e_j$ enters vertex $i$, and 0 otherwise.
An orientation of an (undirected) graph $G = (V, E)$ is the choice of a direction for each of its edges, turning it into a digraph.
Definition (Oriented Incidence Matrix): An oriented incidence matrix of an (undirected) graph $G = (V, E)$ is the incidence matrix of an orientation of $G$. $\lhd$
Example: Here is an example of an orientation:
NUMERICAL CORNER Using LightGraphs.jl, the adjacency matrix of a graph can be obtained with adjacency_matrix. By default, it returns a SparseArrays array, which can be converted to a regular array with Array.
#Julia version: 1.5.1
using LightGraphs, GraphPlot, LinearAlgebra
g = complete_graph(3)
A = adjacency_matrix(g)
Array(A)
g = smallgraph(:petersen)
A = Array(adjacency_matrix(g))
The incidence matrix is obtained with incidence_matrix - again as a SparseArrays.
Array(incidence_matrix(g))
3.2 Laplacian matrix¶
Our main matrix of interest is the Laplacian matrix. It is a graph analogue of the Laplace-Beltrami operator in differential geometry. We will show in particular that it contains useful information about the connectedness of the graph.
3.2.1 Definition and basic properties¶
Recall that, given a graph $G = (V, E)$, the quantity $\delta(v)$ denotes the degree of $v \in V$. The key definition is the following.
Definition (Laplacian Matrix): Let $G = (V,E)$ be a graph with vertices $V = \{1, \ldots, n\}$ and adjacency matrix $A \in \mathbb{R}^{n \times n}$. Let $D = \mathrm{diag}(\delta(1), \ldots, \delta(n))$ be the degree matrix. The Laplacian matrix associated to $G$ is defined as $L = D - A$. Its entries are
$$ l_{ij} = \begin{cases} \delta(i) & \text{if $i = j$}\\ -1 & \text{if $\{i,j\} \in E$}\\ 0 & \text{o.w.} \end{cases} $$$\lhd$
Observe that the Laplacian matrix $L$ of a graph $G$ is symmetric:
$$ L^T = (D- A)^T = D^T - A^T = D - A $$where we used that both $D$ and $A$ are themselves symmetric. The associated quadratic form is particularly simple and will play an important role.
Lemma (Laplacian Quadratic Form): Let $G = (V, E)$ be a graph with $n = |V|$ vertices. Its Laplacian matrix $L$ is positive semi-definite and furthermore we have the following formula for the Laplacian quadratic form
$$ \mathbf{x}^T L \mathbf{x} = \sum_{e = \{i,j\} \in E} (x_i - x_j)^2 $$for any $\mathbf{x} = (x_1, \ldots, x_n)^T \in \mathbb{R}^n$.
Proof: Let $B$ be an oriented incidence matrix of $G$. We claim that $L = B B^T$. Indeed, for $i \neq j$, entry $(i,j)$ of $B B^T$ is a sum over all edges containing $i$ and $j$ as endvertices, of which there is at most one. When $\{i,j\} \in E$, that entry is $-1$, since one of $i$ or $j$ has a $1$ in the column of $B$ corresponding to $e$ and the other one has a $-1$. For $i = j$, letting $b_{xy}$ be entry $(x,y)$ of $B$,
$$ (B B^T)_{ii} = \sum_{e = \{x, y\} \in E: i \in e} b_{xy}^2 = \delta(i). $$Thus, for any $\mathbf{x}$, we have $(B^T \mathbf{x})_k = x_v - x_u$ if the edge $e_k = \{u, v\}$ is oriented as $(u,v)$ under $B$. That implies
$$ \mathbf{x}^T L \mathbf{x} = \mathbf{x}^T B B^T \mathbf{x} = \|B^T \mathbf{x}\|^2 = \sum_{e = \{i,j\} \in E} (x_i - x_j)^2. $$Since the latter is always nonnegative, it also implies that $L$ is positive semidefinite. $\square$
As a convention, we denote the eigenvalues of a Laplacian matrix $L$ by
$$ 0 \leq \mu_1 \leq \mu_2 \leq \cdots \leq \mu_n. $$Another important observation:
Lemma ($\mu_1 = 0$): Let $G = (V, E)$ be a graph with $n = |V|$ vertices and Laplacian matrix $L$. The constant unit vector
$$ \mathbf{y}_1 = \frac{1}{\sqrt{n}} (1, \ldots, 1)^T $$is an eigenvector of $L$ with eigenvalue $0$.
Proof: Let $B$ be an oriented incidence matrix of $G$ recall that $L = B B^T$. By construction $B^T \mathbf{y}_1 = \mathbf{0}$ since each column of $B$ has exactly one $1$ and one $-1$. So $L \mathbf{y}_1 = B B^T \mathbf{y}_1 = \mathbf{0}$ as claimed. $\square$
In general, the constant vector may not be the only eigenvector with eigenvalue one.
Exercise: Let $G$ be a graph with two connected components. Show that its Laplacian $L$ has at least two linearly independent unit eigenvectors with eigenvalue zero. [Hint: Write $L$ as a block matrix and use the lemma above.] $\lhd$
By our proof of the Spectral Theorem, the largest eigenvalue $\mu_n$ of the matrix Laplacian $L$ is the solution to the optimization problem
$$ \mu_n = \max\{\langle \mathbf{x}, L \mathbf{x}\rangle:\|\mathbf{x}\| = 1\}. $$Such extremal characterization is useful in order to bound the eigenvalue $\mu_n$, since any choice of $\mathbf{x}$ with $\|\mathbf{x}\| =1$ gives a lower bound through the quantity $\langle \mathbf{x}, L \mathbf{x}\rangle$. That perspective will be key to our application to graph partitioning.
For now, we give a simple consequence.
Lemma (Laplacian and Degree): Let $G = (V, E)$ be a graph with maximum degree $\bar{\delta}$. Let $\mu_n$ be the largest eigenvalue of its matrix Laplacian $L$. Then
$$ \mu_n \geq \bar{\delta}+1. $$Proof idea: As explained before the statement of the lemma, it suffices to find a good test unit vector $\mathbf{x}$ to plug into $\langle \mathbf{x}, L \mathbf{x}\rangle$. A clever choice does the trick.
Proof: Let $u \in V$ be a vertex with degree $\bar{\delta}$. Let $\mathbf{z}$ be the vector with entries
$$ z_i = \begin{cases} \bar{\delta} & \text{if $i = u$}\\ -1 & \text{if $\{i,u\} \in E$}\\ 0 & \text{o.w.} \end{cases} $$and let $\mathbf{x}$ be the unit vector $\mathbf{z}/\|\mathbf{z}\|$. By definition of the degree of $u$, $\|\mathbf{z}\|^2 = \bar{\delta}^2 + \bar{\delta}(-1)^2 = \bar{\delta}(\bar{\delta}+1)$.
Using the Laplacian Quadratic Form Lemma,
$$ \langle \mathbf{z}, L \mathbf{z}\rangle = \sum_{e = \{i, j\} \in E} (z_i - z_j)^2 \geq \sum_{i: \{i, u\} \in E} (z_i - z_u)^2 = \sum_{i: \{i, u\} \in E} (-1 - \bar{\delta})^2 = \bar{\delta} (\bar{\delta}+1)^2 $$where we restricted the sum to those edges incident with $u$ and used the fact that all terms in the sum are nonnegative. Finally
$$ \langle \mathbf{x}, L \mathbf{x}\rangle = \left\langle \frac{\mathbf{z}}{\|\mathbf{z}\|}, L \frac{\mathbf{z}}{\|\mathbf{z}\|}\right\rangle = \frac{1}{\|\mathbf{z}\|^2} \langle \mathbf{z}, L \mathbf{z}\rangle = \frac{\bar{\delta} (\bar{\delta}+1)^2}{\bar{\delta}(\bar{\delta}+1)} = \bar{\delta}+1 $$so that
$$ \mu_n = \max\{\langle \mathbf{x}', L \mathbf{x}'\rangle:\|\mathbf{x}'\| = 1\} \geq \langle \mathbf{x}, L \mathbf{x}\rangle = \bar{\delta}+1 $$as claimed. $\square$
3.2.2 Extremal Characterization of $\mu_2$¶
A special case of Courant-Fischer for the Laplacian is the following.
Corollary (Extremal Characterization of $\mu_2$): Let $G = (V, E)$ be a graph with $n = |V|$ vertices. Assume the Laplacian $L$ of $G$ has spectral decomposition $L = \sum_{i=1}^n \mu_i \mathbf{y}_i \mathbf{y}_i^T$ with $0 = \mu_1 \leq \mu_2 \leq \cdots \leq \mu_n$ and $\mathbf{y}_1 = \frac{1}{\sqrt{n}}(1,\ldots,1)^T$. Then
$$ \mu_2 = \min\left\{ \frac{\sum_{\{u, v\} \in E} (x_u - x_v)^2}{\sum_{u = 1}^n x_u^2} \,:\, \mathbf{x} = (x_1, \ldots, x_n)^T \neq \mathbf{0}, \sum_{u=1}^n x_u = 0 \right\}. $$Proof: By Courant-Fischer,
$$ \mu_2 = \min_{\mathbf{x} \in \mathcal{W}_{d-1}} \mathcal{R}_L(\mathbf{x}). $$Since $\mathbf{y}_1$ is constant and $\mathcal{W}_{d-1}$ the subspace orthogonal to it, this is equivalent to restrictring the minimization to those non-zero $\mathbf{x}$'s such that
$$ 0 = \langle \mathbf{x}, \mathbf{y}_1 \rangle = \frac{1}{\sqrt{n}} \sum_{u=1}^m x_u. $$Moreover, by the Laplacian Quadratic Form Lemma,
$$ \langle \mathbf{x}, L \mathbf{x}\rangle = \sum_{\{u, v\} \in E} (x_u - x_v)^2 $$so the Rayleigh quotient is
$$ \mathcal{R}_L(\mathbf{x}) = \frac{\langle \mathbf{x}, L \mathbf{x} \rangle}{\langle \mathbf{x}, \mathbf{x} \rangle} = \frac{\sum_{\{u, v\} \in E} (x_u - x_v)^2}{\sum_{u = 1}^n x_u^2}. $$That proves the claim. $\square$
One application of this extremal characterization is a graph drawing heuristic. Consider the entries of the second Laplacian eigenvector $\mathbf{y}_2$ normalized to have unit norm. The entries are centered around $0$ by the condition $\sum_{u=1}^n x_{u} = 0$. Because it minimizes the quantity
$$ \frac{\sum_{\{u, v\} \in E} (x_u - x_v)^2}{\sum_{u = 1}^n x_u^2} $$over all centered unit vectors, $\mathbf{y}_2$ tends to assign similar coordinates to adjacent vertices. A similar reasoning applies to the third Laplacian eigenvector, which in addition is orthogonal to the second one.
NUMERICAL CORNER As we said, one use of the spectral decomposition of the Laplacian matrix is in graph drawing. We illustrate this next. Given a graph $G = (V, E)$, it is not clear a priori how to draw it in the plane since the only information available are adjacencies of vertices. One approach is just to position the vertices at random. The function gplot provides a functionality to supply a layout function that returns an $x$ and $y$-coordinate for each vertex.
We will test this on a grid graph. Sometimes a picture is worth a thousand words. This is an example of a $4 \times 7$-grid graph.
(Source)
We use grid to construct such a graph.
g = grid([4,7])
Next, we write a function that returns independent uniform coordinates in $[0,1]$ for the vertices.
function rand_locs(g)
return rand(nv(g)), rand(nv(g)) # random x and y coord for each vertex
end
Here is what it looks like on the graph g. Each row below gives the $x$ and $y$-coordinates of one vertex.
(x, y) = rand_locs(g)
hcat(x,y)
Providing these coordinates to gplot through the layout option gives the following drawing of the graph.
gplot(g, layout=rand_locs)
Clearly, this is a lot harder to read than the original graph above.
Another approach is to map the vertices to two eigenvectors, similarly to what we did for dimensionality reduction. The eigenvector associated to $\mu_1$ is constant and therefore not useful for drawing. We try the next two. We use laplacian_matrix to compute the Laplacian matrix of the graph. By default, the function eigen, lists eigenvalues in increasing order (if they real).
function spec_locs(g)
L = Array(laplacian_matrix(g)) # laplacian L of g
F = eigen(L) # spectral decomposition
v = F.vectors # eigenvectors
return v[:,2], v[:,3] # returns 2nd and 3rd eigenvectors
end
gplot(g, layout=spec_locs)
Interestingly, the outcome is very similar to the original, more natural drawing.