REVIEW

Matrix norms and singular value decomposition

Course: Math 888 - High-Dimensional Probability and Statistics (HDPS)
Author: Sebastien Roch, Department of Mathematics, University of Wisconsin-Madison
Updated: Sep 27, 2021
Copyright: © 2021 Sebastien Roch

1 Matrix norms

Recall that the Frobenius norm of an $n \times m$ matrix $A \in \mathbb{R}^{n \times m}$ is defined as

$$ \|A\|_F = \sqrt{\sum_{i=1}^n \sum_{j=1}^m a_{ij}^2}. $$

The Frobenius norm does not directly relate to $A$ as a representation of a linear map. In particular, it is desirable in many contexts to quantify how two matrices differ in terms of how they act on vectors.

For instance, one is often interested in bounding quantities of the following form. Let $B, B' \in \mathbb{R}^{n \times m}$ and let $\mathbf{x} \in \mathbb{R}^m$ be of unit norm. What can be said about $\|B \mathbf{x} - B' \mathbf{x}\|$? Intuitively, what we would like is this: if the norm of $B - B'$ is small then $B$ is close to $B'$ as a linear map, that is, the vector norm $\|B \mathbf{x} - B' \mathbf{x}\|$ is small for any unit vector $\mathbf{x}$. The following definition provides us with such a notion. Define $\mathbb{S}^{m-1} = \{\mathbf{x} \in \mathbb{R}^m\,:\,\|\mathbf{x}\| = 1\}$.

Definition (Induced Norm): The $2$-norm of a matrix $A \in \mathbb{R}^{n \times m}$ is

$$ \|A\|_2 = \max_{\mathbf{0} \neq \mathbf{x} \in \mathbb{R}^m} \frac{\|A \mathbf{x}\|}{\|\mathbf{x}\|} = \max_{\mathbf{x} \in \mathbb{S}^{m-1}} \|A \mathbf{x}\|. $$

$\lhd$

The equality in the definition uses the homogeneity of the vector norm. Also the definition implicitly uses the Extreme Value Theorem. In this case, we use the fact that the function $f(\mathbf{x}) = \|A \mathbf{x}\|$ is continuous and the set $\mathbb{S}^{m-1}$ is closed and bounded to conclude that there exists $\mathbf{x}^* \in \mathbb{S}^{m-1}$ such that $f(\mathbf{x}^*) \geq f(\mathbf{x})$ for all $\mathbf{x} \in \mathbb{S}^{m-1}$.

Exercise: Let $A \in \mathbb{R}^{n \times m}$. Use Cauchy-Schwarz to show that

$$ \|A\|_2 = \max \left\{ \mathbf{x}^T A \mathbf{y} \,:\, \|\mathbf{x}\| = \|\mathbf{y}\| = 1 \right\}. $$

$\lhd$

Exercise: Let $A \in \mathbb{R}^{n \times m}$.

(a) Show that $\|A\|_F^2 = \sum_{j=1}^m \|A \mathbf{e}_j\|^2$.

(b) Use (a) and Cauchy-Schwarz to show that $\|A\|_2 \leq \|A\|_F$.

(c) Give an example such that $\|A\|_F = \sqrt{n} \|A\|_2$. $\lhd$

The $2$-norm of a matrix has many other useful properties.

Lemma (Properties of the Induced Norm): Let $A, B \in \mathbb{R}^{n \times m}$ and $\alpha \in \mathbb{R}$. The following hold:

(a) $\|A \mathbf{x}\| \leq \|A\|_2 \|\mathbf{x}\|$, $\forall \mathbf{0} \neq \mathbf{x} \in \mathbb{R}^m$

(b) $\|A\|_2 \geq 0$

(c) $\|A\|_2 = 0$ if and only if $A = 0$

(d) $\|\alpha A\|_2 \leq |\alpha| \|A\|_2$

(e) $\|A + B \|_2 \leq \|A\|_2 + \|B\|_2$

(f) $\|A B \|_2 \leq \|A\|_2 \|B\|_2$.

Proof: These properties all follow from the definition of the induced norm and the corresponding properties for the vector norm:

  • Claims (a) and (b) are immediate from the definition.

  • For (c) note that $\|A\|_2 = 0$ implies $\|A \mathbf{x}\|_2 = 0, \forall \mathbf{x} \in \mathbb{S}^{m-1}$, so that $A \mathbf{x} = \mathbf{0}, \forall \mathbf{x} \in \mathbb{S}^{m-1}$. In particular, $a_{ij} = \mathbf{e}_i^T A \mathbf{e}_j = 0, \forall i,j$.

  • For (d), (e), (f), observe that for all $\mathbf{x} \in \mathbb{S}^{m-1}$

$$ \|\alpha A \mathbf{x}\| = |\alpha| \|A \mathbf{x}\| $$$$\|(A+B)\mathbf{x}\| = \|A\mathbf{x} + B\mathbf{x}\| \leq \|A\mathbf{x}\| + \|B\mathbf{x}\| \leq \|A\|_2 + \|B\|_2 $$$$ \|(AB)\mathbf{x}\| = \|A(B\mathbf{x})\| \leq \|A\|_2 \|B\mathbf{x}\| \leq \|A\|_2 \|B\|_2.$$

$\square$

Exercise: Use Cauchy-Schwarz to show that for any $A, B$ it holds that

$$ \|A B \|_F \leq \|A\|_F \|B\|_F. $$

$\lhd$

2 Singular Value Decomposition

First recall a matrix $D \in \mathbb{R}^{n \times m}$ is diagonal if its non-diagonal entries are zero. That is, $i \neq j$ implies that $D_{ij} =0$. We now come to our main definition.

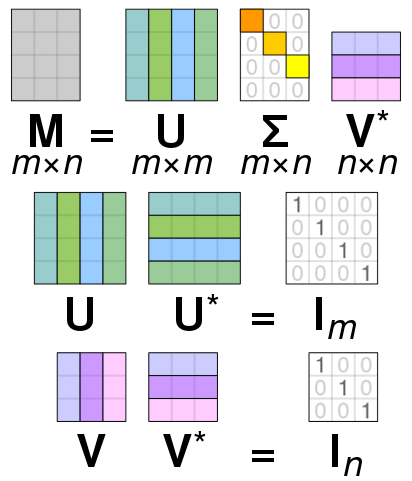
Definition (Singular Value Decomposition): Let $A \in \mathbb{R}^{n\times m}$ be a matrix with $m \leq n$. A singular value decomposition (SVD) of $A$ is a matrix factorization

$$ A = U \Sigma V^T = \sum_{j=1}^r \sigma_j \mathbf{u}_j \mathbf{v}_j^T $$

where the columns of $U \in \mathbb{R}^{n \times r}$ and those of $V \in \mathbb{R}^{m \times r}$ are orthonormal, and $\Sigma \in \mathbb{R}^{r \times r}$ is a diagonal matrix. Here the $\mathbf{u}_j$'s are the columns of $U$ and are referred to as left singular vectors. Similarly the $\mathbf{v}_j$'s are the columns of $V$ and are referred to as right singular vectors. The $\sigma_j$'s, which are non-negative and in decreasing order

$$ \sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r > 0 $$

are the diagonal elements of $\Sigma$ and are referred to as singular values. $\lhd$

This type of matrix factorization is illustrated below (in its full form).

SVD

(Source)

Exercise: Let $A = U \Sigma V^T = \sum_{j=1}^r \sigma_j \mathbf{u}_j \mathbf{v}_j^T$ be an SVD of $A$.

(a) Show that $\{\mathbf{u}_j:j\in[r]\}$ is a basis of $\mathrm{col}(A)$ and that $\{\mathbf{v}_j:j\in[r]\}$ is a basis of $\mathrm{row}(A)$.

(b) Show that $r$ is the rank of $A$. $\lhd$

Remarkably, any matrix has an SVD.

Theorem (Existence of SVD): Any matrix $A \in \mathbb{R}^{n\times m}$ has a singular value decomposition.

The construction works as follows. Compute the greedy sequence $\mathbf{v}_1,\ldots,\mathbf{v}_r$ from the previous section until the first $r$ such that

$$ \max \{\|A \mathbf{v}\|:\|\mathbf{v}\| = 1, \ \langle \mathbf{v}, \mathbf{v}_j \rangle = 0, \forall j \leq r\} = 0 $$

or, otherwise, until $r=m$. The $\mathbf{v}_j$'s are orthonormal by construction. For $j=1,\ldots,m$, let

$$ \sigma_j = \|A \mathbf{v}_j\| \quad\text{and}\quad \mathbf{u}_j = \frac{1}{\sigma_j} A \mathbf{v}_j. $$

Observe that, by our choice of $r$, the $\sigma_j$'s are $> 0$. In particular, the $\mathbf{u}_j$'s have unit norm by definition. See Math 535 notes for more details.

3 Low-rank approximation in the induced norm

Let $A \in \mathbb{R}^{n \times m}$ be a matrix with SVD

$$ A = \sum_{j=1}^r \sigma_j \mathbf{u}_j \mathbf{v}_j^T. $$

For $k < r$, truncate the sum at the $k$-th term

$$ A_k = \sum_{j=1}^k \sigma_j \mathbf{u}_j \mathbf{v}_j^T. $$

The rank of $A_k$ is exactly $k$. Indeed, by construction,

  1. the vectors $\{\mathbf{u}_j\,:\,j = 1,\ldots,k\}$ are orthonormal, and

  2. since $\sigma_j > 0$ for $j=1,\ldots,k$ and the vectors $\{\mathbf{v}_j\,:\,j = 1,\ldots,k\}$ are orthonormal, $\{\mathbf{u}_j\,:\,j = 1,\ldots,k\}$ spans the column space of $A_k$.

We have shown before (see Math 535 notes) that $A_k$ is the best approximation to $A$ among matrices of rank at most $k$ in Frobenius norm. Specifically, the Greedy Finds Best Fit Theorem implies that, for any matrix $B \in \mathbb{R}^{n \times m}$ of rank at most $k$,

$$ \|A - A_k\|_F \leq \|A - B\|_F. $$

We show in this section that the same holds in the induced norm. First, some observations.

Lemma (Matrix Norms and Singular Values): Let $A \in \mathbb{R}^{n \times m}$ be a matrix with SVD

$$ A = \sum_{j=1}^r \sigma_j \mathbf{u}_j \mathbf{v}_j^T $$

where recall that $\sigma_1 \geq \sigma_2 \geq \cdots \sigma_r > 0$ and let $A_k$ be the truncation defined above. Then

$$ \|A - A_k\|^2_F = \sum_{j=k+1}^r \sigma_j^2 $$

and

$$ \|A - A_k\|^2_2 = \sigma_{k+1}^2. $$

Proof: For the first claim, by definition, summing over the columns of $A - A_k$

$$ \|A - A_k\|^2_F = \left\|\sum_{j=k+1}^r \sigma_j \mathbf{u}_j \mathbf{v}_j^T\right\|_F^2 = \sum_{i=1}^m \left\|\sum_{j=k+1}^r \sigma_j v_{j,i} \mathbf{u}_j \right\|^2. $$

Because the $\mathbf{u}_j$'s are orthonormal, this is

$$ \sum_{i=1}^m \sum_{j=k+1}^r \sigma_j^2 v_{j,i}^2 = \sum_{j=k+1}^r \sigma_j^2 \left(\sum_{i=1}^m v_{j,i}^2\right) = \sum_{j=k+1}^r \sigma_j^2 $$

where we used that the $\mathbf{v}_j$'s are also orthonormal.

For the second claim, recall that the induced norm is defined as

$$ \|B\|_2 = \max_{\mathbf{x} \in \mathbb{S}^{m-1}} \|B \mathbf{x}\|. $$

For any $\mathbf{x} \in \mathbb{S}^{m-1}$

$$ \left\|(A - A_k)\mathbf{x}\right\|^2 = \left\| \sum_{j=k+1}^r \sigma_j \mathbf{u}_j (\mathbf{v}_j^T \mathbf{x}) \right\|^2 = \sum_{j=k+1}^r \sigma_j^2 \langle \mathbf{v}_j, \mathbf{x}\rangle^2. $$

Because the $\sigma_j$'s are in decreasing order, this is maximized when $\langle \mathbf{v}_j, \mathbf{x}\rangle = 1$ if $j=k+1$ and $0$ otherwise. That is, we take $\mathbf{x} = \mathbf{v}_{k+1}$ and the norm is then $\sigma_{k+1}^2$, as claimed. $\square$

Theorem (Low-Rank Approximation in the Induced Norm): Let $A \in \mathbb{R}^{n \times m}$ be a matrix with SVD

$$ A = \sum_{j=1}^r \sigma_j \mathbf{u}_j \mathbf{v}_j^T $$

and let $A_k$ be the truncation defined above with $k < r$. For any matrix $B \in \mathbb{R}^{n \times m}$ of rank at most $k$,

$$ \|A - A_k\|_2 \leq \|A - B\|_2. $$

Proof idea: We know that $\|A - A_k\|_2^2 = \sigma_{k+1}^2$. So we want to lower bound $\|A - B\|_2^2$ by $\sigma_{k+1}^2$. For that, we have to find an appropriate $\mathbf{z}$ for any given $B$ of rank at most $k$. The idea is to take a vector $\mathbf{z}$ in the intersection of the null space of $B$ and the span of the singular vectors $\mathbf{v}_1,\ldots,\mathbf{v}_{k+1}$. By the former, the squared norm of $(A - B)\mathbf{z}$ is equal to the squared norm of $A\mathbf{z}$ which lower bounds $\|A\|_2^2$. By the latter, $\|A \mathbf{z}\|^2$ is at least $\sigma_{k+1}^2$.