Data Relationships

Definitions:
response variable - measures an outcome or result of a study (y-axis)
explanatory variable - variable that may cause changes in response variables (x-axis)

A scatterplot describes datapoints relating two variables. (see p. 224)

We look for:

-    overall pattern
-    form
-    direction
-    strength of relationship
-    deviations, in particular
-    outliers

Two variables are positively correlated if they grow bigger together.
They are negatively correlated if, as one grows, the other declines.

examples:

height - weight
weight of vehicle - gas mileage
length of name - head circumference
height above sea level - temperature

A regression line - line that describes how variable y changes as variable x changes.
(Can you draw an approximation line through the data points in the scatter plot? How good an approximation is it?)
see p. 227

line equation: y = ax + b,
where a = slope,
b = y-intercept

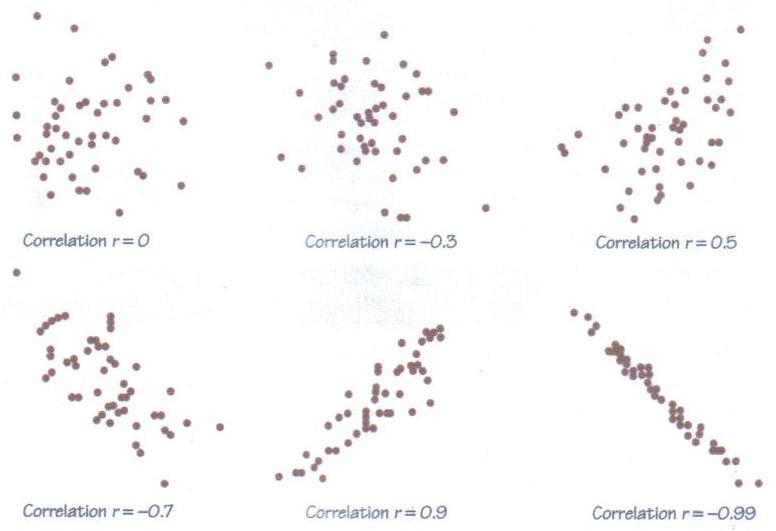
The correlation r is a number between -1 and 1:

r > 0     positively correlated
r < 0    negatively correlated
|r| close to 1    strongly correlated, i.e. points lie close to a line or on it.
|r| close to 0    weakly correlated, i.e. points lie scattered, line not very discernible
r = 0    no straight line relationship

Computing r:
Given data points (x₁, y₁), , (x_n, y_n), means m_x , m_y and standard deviations s_x , s_y.
Then

r = 1/(n-1) [(x₁ - m_x)(y₁ - m_y)/s_xs_y + ... + (x_n - m_x)(y_n - m_y)/s_xs_y]

the least squares regression line: y = ax + b,

where a = r * (s_y/ s_x)
and b = m_y - a m_x

Archeopterix example:

Femur length x	38	56	59	64	74
Humerus length y	41	63	70	72	84

Plot the data points
compute the correlation,

is it a weak/strong correlation?
positive/negative correlation?

compute the regression line
suppose you find a humerus of length 68 belonging to an archeopterix, how long do you estimate the femur of that individual would have to be?

Outliers and Correlation/Regression:

x	1	1	4	5	6	7	8	9
y	1	3	1	4	2	3	1	2

compute the correlation

a) add an outlier (x,y) = (30,40) as a data value to the above list

compute the correlation,

is it a weak/strong correlation?
positive/negative correlation?

compute the regression line

b) add instead the outlier (x,y) = (30, - 40) as a data value to the above list

compute the correlation,

is it a weak/strong correlation?
positive/negative correlation?

compute the regression line

Correlation does not imply causation.
Examples:

ice cream parlor next to public pool does a business in summer:
underlying cause: heat in summer causes both crowds at the pool and the icecream parlor.
child is ill with fever and a bad cough. Treatment with Tylenol doesn't work.
Obviously, fever and cough are related. Fever is the bodies reaction to fight a disease whose other symptom is cough.
One such disease is pneumonia, the underlying cause.
So it's not enough to treat the symptoms, one has to treat the disease.

In the law:

possible cause is indicated by a correlation, which leads to investigation
probable cause is given, when the correlation involves cause, which is needed for a warrant or a wiretap
cause beyond reasonable doubt: found a physical model explaining the situation. Usual standard for conviction.