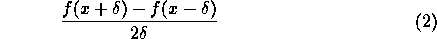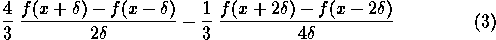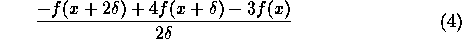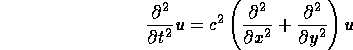Problem set 2 Due: Tuesday, Sept. 29, 1998
1. Design of experiments and data analysis
Determine experimentally the order of accuracy of the
finite difference formulas given below
(i.e. how does the error scale with
 ).
Also, determine the optimum
).
Also, determine the optimum  for each formula. Based on your
limited data, can you suggest a relation between machine precision
eps and
for each formula. Based on your
limited data, can you suggest a relation between machine precision
eps and  ?
You must explain your approach to solving this problem.
?
You must explain your approach to solving this problem.

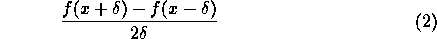
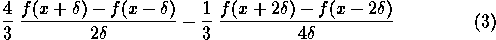
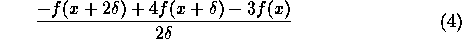
2.
The vibrations of an elastic drum (or membrane) are governed by the partial differential
equation (called the wave equation)
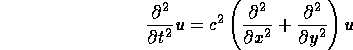
where u(x,y,t) is the elevation of the membrane which depends on
position x,y and time t.
The parameter c2 depends on material properties.
The wave equation has solutions that are periodic in time
and do not change shape, called ``eigenmodes''.
A circular drum has axisymmetric eigenmodes of
the form 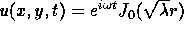 where
where
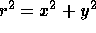 and
and
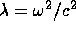 , with
, with
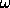 the ``eigenfrequency" (also called ``characteristic'' frequency).
If the drum is attached around its rim, then we must have
the ``eigenfrequency" (also called ``characteristic'' frequency).
If the drum is attached around its rim, then we must have
 where R is the radius of the drum.
where R is the radius of the drum.
- Find the first 20 eigenfrequencies of
a circular drum with R= 1 and c2 = 1.
- Plot the spatial shape of the third eigenmode of vibration.
Hint: the function
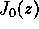 is
the Bessel function of the first kind of order 0.
Asymptotic analysis for large z tells us that
is
the Bessel function of the first kind of order 0.
Asymptotic analysis for large z tells us that
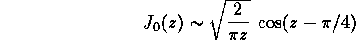
Bessel functions are very important in Science and Engineering.
They appear for diffusion and wave problems in cylindrical geometry.
This problem 3 is NOT due Tuesday Sept 29. It will be due later.
3. Consider a chain of 23 identical masses Mj ,
j=1,...,23
connected to each other by 22 identical springs, with spring constant K
and rest length L ,
and to fixed extremities by two additional springs identical to the other 22.
The length of the chain from one fixed extremity to the other is 24 L .
If the force on mass Mj is Fj = j(j-24)
find the displacement of each mass from its rest position. Display your results
in reader-friendly way (and especially, GRADER-friendly...).
Fabian Waleffe
Wed Sep 16 12:46:19 CDT 1998
Mon Sep 21 15:39:25 CDT 1998
 ).
Also, determine the optimum
).
Also, determine the optimum  for each formula. Based on your
limited data, can you suggest a relation between machine precision
eps and
for each formula. Based on your
limited data, can you suggest a relation between machine precision
eps and  ?
You must explain your approach to solving this problem.
?
You must explain your approach to solving this problem.