% This is a sequence of Matlab commands to get you started in CAECC
% (Computer Aided Exploration of Complex Calculus).
% Start Matlab then cut-and-paste. The Matlab output is shown below.
% F. Waleffe for Math 321, Apr 12, 2010
i=sqrt(-1)
z = -2 - i/2^6
disp('[real(z), imag(z)]'),
[real(z), imag(z)]          % real and imaginary parts of z
disp('[abs(z), angle(z)]'),
[abs(z), angle(z)]          % modulus and argument of z
zstar=conj(z); zstar        % conjugate of z
[abs(zstar), angle(zstar)]  % modulus and argument of z*
disp('[ln(z), ln(z*)]'),
[log(z), log(zstar)]        % Matlab's ln(z) and ln(z*)

(2+3*i)^(6+2*i)             % complex power of a complex number

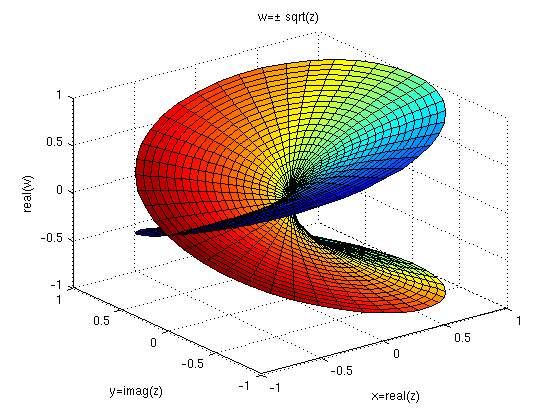
figure(1), cplxroot(2)      % Riemann surface
xlabel('x=real(z)'), ylabel('y=imag(z)'),zlabel('real(w)'), title('w=\pm sqrt(z)')
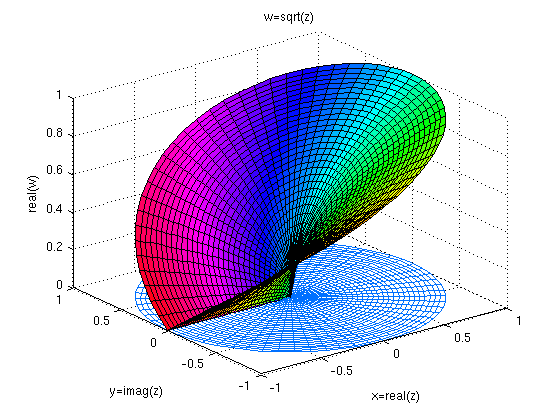
z=cplxgrid(30);
figure(2), cplxmap(z,sqrt(z))   % Matlab's definition of sqrt(z)
xlabel('x=real(z)'), ylabel('y=imag(z)'),zlabel('real(w)'), title('w=sqrt(z)')

% OK, you typed it all, but of course you want to digest the results.
% Do they make sense to you? What's Matlab doing?

% there is more, see
help cplxdemo

i =

        0 + 1.0000i


z =

  -2.0000 - 0.0156i

[real(z), imag(z)]

ans =

   -2.0000   -0.0156

[abs(z), angle(z)]

ans =

    2.0001   -3.1338


zstar =

  -2.0000 + 0.0156i


ans =

    2.0001    3.1338

[ln(z), ln(z*)]

ans =

   0.6932 - 3.1338i   0.6932 + 3.1338i


ans =

  -1.7572e+02 + 2.5264e+02i

  Functions of Complex Variables
  MATLAB(R) can help you perform some very interesting manipulations on complex
  variable.
 
  Copyright 1984-2007 The MathWorks, Inc.
  $Revision: 5.10.4.2 $ $Date: 2007/12/14 14:51:01 $

    Published output in the Help browser
       showdemo cplxdemo

Published with MATLAB® 7.9