cplxlect30

% Visualizing complex functions in Matlab: a quick intro.
% Math 321, F. Waleffe Apr 16, 2010

r=[0:1/2^5:1]';               % defines a column of r values from 0 to 1
theta=[0:1/2^6:1]*2*pi;       % defines a row of theta values from 0 to 2 &pi;
i=sqrt(-1);                   % makes sure you did not redefine "i"
z=r*exp(i*theta);             % defines our own "cplxgrid" of z values
x=real(z); y=imag(z);

%Visualizing w=z^2 (see notes also)

w=z.^2; u=real(w); v=imag(w);
figure(1), cplxmap(z,w)   % 3D color plot of z^2
colormap(jet)

help cplxmap                  % tells you about `cplxmap'
xlabel('x'), ylabel('y'), title('w=z^2')
caxis([-1 1]), colorbar

figure(2), contourf(x,y,u), axis image, xlabel('x'), ylabel('y'), title('contours of u=real(z^2)')
colorbar
figure(3), contourf(x,y,v), axis image, xlabel('x'), ylabel('y'), title('contours of v=imag(z^2)')
colorbar

%------------------------------------------------------------------------
% Matlab's sqrt(z)

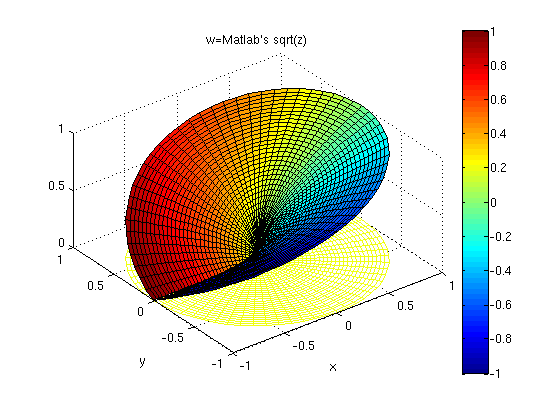
figure(4), cplxmap(z,sqrt(z)) % plots all w's such that w=matlab's sqrt(z)
colormap(jet)
xlabel('x'), ylabel('y') , title('w=Matlab''s sqrt(z)')
caxis([-1 1]), colorbar, axis image

% My sqrt(z)
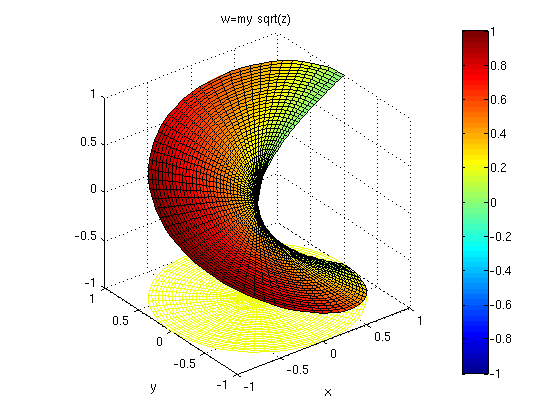
myrtz=sqrt(r)*exp(i*theta/2); % defines my sqrt(z)

figure(5), cplxmap(z,myrtz)   % plots all w's such that w=my sqrt(z)
colormap(jet)
xlabel('x'), ylabel('y'), title('w=my sqrt(z)'), axis image
caxis([-1 1]), colorbar

% Riemann surface for sqrt(z)
theta2=[0:1/2^6:2]*2*pi; z2=r*exp(i*theta2);   % twice around the origin!
figure(6), cplxmap(z2,sqrt(r)*exp(i*theta2/2)) % plots all w's such that w^2=z
colormap(jet)
xlabel('x'), ylabel('y'), title('w such that w^2=z'), axis image
caxis([-1 1]), colorbar

% compare figures 4, 5 and 6. They are showing the "same" function.

 CPLXMAP Plot a function of a complex variable.
    CPLXMAP(z,f(z),(optional bound))
    Used by CPLXDEMO.
 
    See also CPLXGRID.