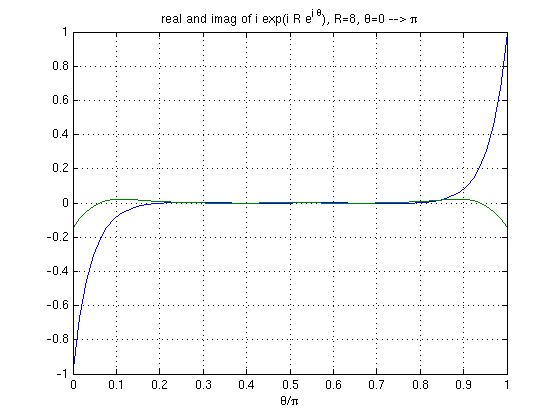
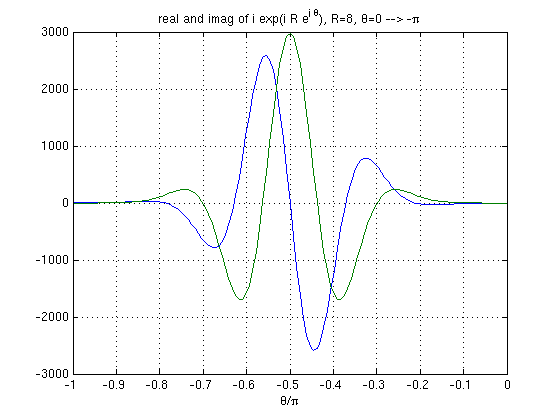
% CLOSING ON TOP OR BOTTOM? for e^(iz)/z. Integral of Sinc(x), JORDAN's Lemma.

% This Matlab file plots [i e^(i z)] over z=R e^(i t)
% This occurs in integral of sin(x)/x from -infinity to infinity by contour
% integration. z=R e^(i t) is the circular path closing the contour. Here
% we consider closing on top (t=0 --> pi) and bottom (t=0 --> -pi)
%
% For z=R e^(it), dz = iR e^(it) dt,
%  so e^(iz)/z dz = exp(iR e^(it)) i dt = exp(i R cos t) exp(-R sin t) i dt
% = -sin(R cos t) exp(-R sin t) dt + i cos(R cos t) exp(-R sin t) dt
%
% You can CUT-and-PASTE into Matlab. Output is plotted below
% F. Waleffe, for Math 321 5/5/2010

% R=input('R=? (not too big, say 8 to start)  ');
% R is going to infinity, but we have to be able to see things!

R=8;

% Closing on top: t = 0 -> pi
t=[0:1/2^6:1]*pi;
repart=-sin(R*cos(t)).*exp(-R*sin(t)); % real( i e^(i z) )
impart= cos(R*cos(t)).*exp(-R*sin(t)); % imag( i e^(i z) )

figure(1)
plot(t/pi,repart,t/pi,impart)
grid, xlabel('\theta/\pi')
Rs=num2str(R);
T=strcat('real and imag of i exp(i R e^{i \theta}), R=',Rs,', \theta=0 --> \pi');
title(T)

% Closing on bottom: t = 0 --> - pi
figure(2)
t=-[0:1/2^7:1]*pi;
repart=-sin(R*cos(t)).*exp(-R*sin(t));
impart=cos(R*cos(t)).*exp(-R*sin(t));
plot(t/pi,repart,t/pi,impart)
grid, xlabel('\theta/\pi')
Rs=num2str(R);
T=strcat('real and imag of i exp(i R e^{i \theta}), R=',Rs,', \theta=0 --> -\pi');
title(T)

disp('NOTE the difference in SCALE on the figures!')
disp('NOW, TRY BIGGER R values')

NOTE the difference in SCALE on the figures!
NOW, TRY BIGGER R values

Published with MATLAB® 7.9