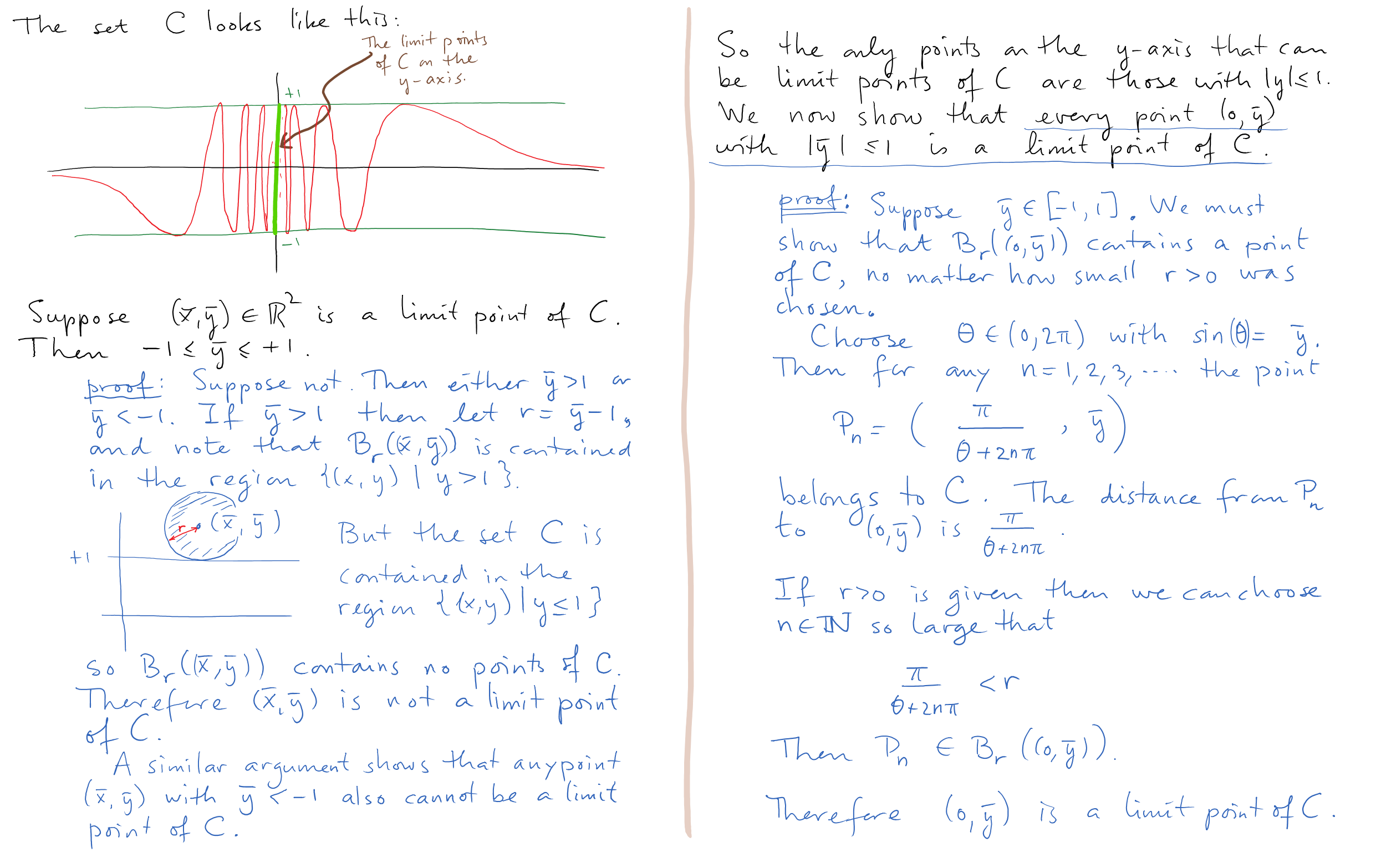
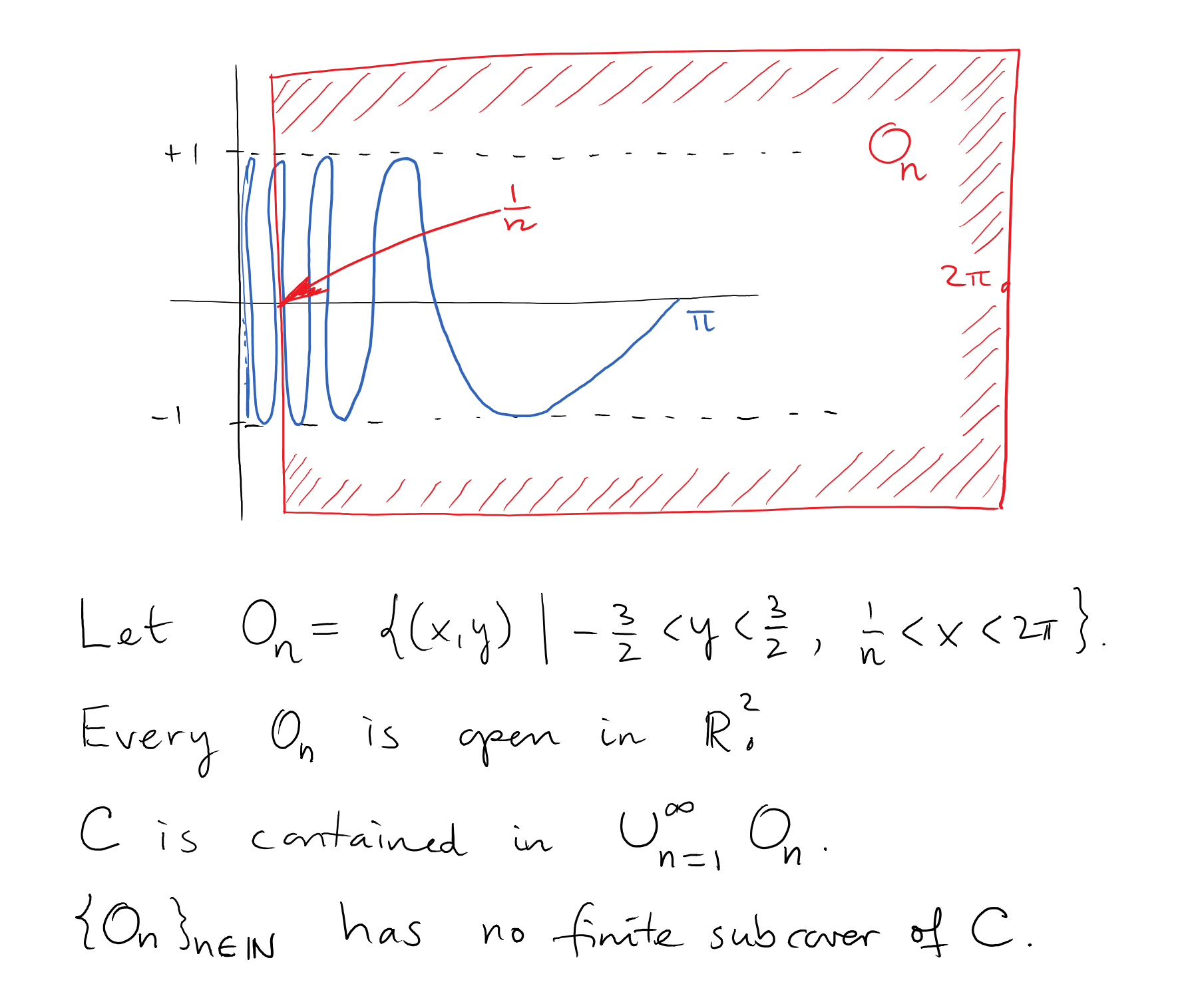
Homework 2 due Monday, February 1.

In this solution the following version of the Archimedean
property is used: for any $x>0$ there is a positive integer
$n\in\mathbb{N}$ such that $10^{-n}\lt x$. That is not exactly
the Archimedean property as stated in Rudin’s book. In fact
proving that this version also is true is practice problem 7a for
the first midterm.
Homework 3
Is $\mathbb Q$ an open subset of $\R$? No. Proof: $0$ is
not an interior point of $\mathbb{Q}$ because every interval $(-r,
r)$ contains an irrational number. (For example, given $r\gt0$,
choose $n\in\mathbb{N}$ so large that $\frac1n\sqrt2 \lt r$.)
Is $\mathbb{Q}$ a closed subset of $\R$? No. For
example, $\sqrt2$ is a limit point of $\mathbb Q$, because every
interval $\bigl(\sqrt2-r, \sqrt2+r\bigr)$ contains a rational number
(Rudin, theorem 1.20b, “$\mathbb Q$ is dense in $\R$”).
Does $\R\setminus\mathbb Q$ have any interior points?
No. Let $x\in\R\setminus\mathbb Q$ be given. Then every interval $(x-r,
x+r)$ contains a rational number, no matter how you choose $r$.
Therefore $x$ is not an interior point of $\R\setminus\mathbb Q$.
Is $\mathbb Z$ an open subset of $\R$? No. We have to
disprove that every point in $\mathbb Z$ is an interior point, so we
only have to show that one of the points in $\mathbb Z$ is not an
interior point. For example, $0$ is not an interior point of
$\mathbb Z$ because any interval $(-r, r)$ contains a noninteger.
Is $\mathbb Z$ a closed subset of $\R$? Yes. It is
easiest to show that $\R\setminus\mathbb Z$ is open. Let
$x\in\R\setminus\mathbb Z$ be given, and let $n$ be the integer for
which $n\lt x\lt n+1$. Choose $r=\min(x-n, n+1-x)$. Then the
interval $(x-r, x+r)$ is a neighborhood of $x$ which is contained in
$\R\setminus\mathbb Z$, so that $x$ is an interior point of
$\R\setminus\mathbb Z$.